Описанная сфера на олимпиадах и ЕГЭ

Содержание

Введение

1 Сфера и шар

1.1 Сфера и шар: основные понятия и определения

1.2 Описанная сфера

1.2.1 Основные свойства и определения

1.2.2 Комбинация с пирамидой

1.2.3 Комбинация с призмой

1.2.4 Комбинация с цилиндром

1.2.5 Комбинация с конусом

2 Примеры олимпиадных заданий

2.1 Примеры олимпиадных заданий с пирамидой

2.2 Примеры ол

импиадных заданий с призмой

2.3 Примеры олимпиадных заданий с цилиндром

2.4 Примеры олимпиадных заданий с конусом

3 Примеры заданий ЕГЭ

3.1 Примеры заданий ЕГЭ с пирамидой

3.2 Примеры заданий ЕГЭ с призмой

3.3 Примеры заданий ЕГЭ с цилиндром

3.4 Примеры заданий ЕГЭ с конусом

Заключение

Список литературы

Приложение. Задачи для самостоятельного решения

Введение

Данная работа выполняется в рамках проекта по созданию математической странички для школьников на сайте лицея-интерната и будет размещена в разделе «Математические методы».

Цель работы – создание справочника, посвященного методу решения геометрических задач с описанной сферой на олимпиадах и ЕГЭ.

Для достижения данной цели нам необходимо было решить следующие задачи:

1) ознакомиться с понятием описанной сферы;

2) изучить особенности комбинаций описанной сферы с пирамидой, призмой, цилиндром и конусом;

3) среди геометрических задач выбрать те, которые содержат условие наличия описанной сферы;

4) проанализировать, систематизировать и проклассифицировать собранный материал;

5) сделать подборку задач для самостоятельного решения;

6) оформить результат исследования в виде реферата.

В процессе исследования мы выяснили, что задачи с описанной сферой достаточно часто предлагаются школьникам на ЕГЭ, поэтому умение решать задачи данного типа играет немало важную роль в успешной сдаче экзаменов. Так же задачи с описанной сферой часто встречаются на олимпиадах по математике различного уровня. Соответствующие примеры приведены в нашей работе. Данная тема является актуальной, так как задачи данного типа обычно вызывают затруднения у школьников.

Практическая значимость – подготовленные нами материалы могут быть использованы при подготовке школьников к олимпиадам, ЕГЭ и последующему обучению в вузе.

1 Сфера и шар

1.1 Сфера и шар: основные понятия и определения

Сферой называется поверхность, состоящая всех точек пространства, расположенных на данном расстоянии от данной точки.

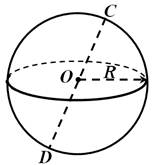
Рис. 1

Данная точка называется центром сферы (точка О на рис. 1), а данное расстояние радиусом сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, так же называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы (отрезок DC на рис. 1). Отметим, что сфера может быть получена вращением полуокружности вокруг её диаметра.

Шаром называется тело, ограниченное сферой. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Очевидно, шар радиуса R с центром в О содержит все точки пространства, которые расположены от точки О на расстоянии, не превышающем R (включая точку О), и не содержит других точек. Шаром также называют фигуру вращения полукруга вокруг его диаметра. Шаровой сегмент – часть шара, отсекаемая от него какой-нибудь плоскостью. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость. Плоскость, проходящая через центра шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью. Шаровой сектор – геометрическое тело, которое получается при вращении кругового сектора с углом, меньшим 90о, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов. Шаровой сектор состоит из шарового сегмента и конуса с общим основанием.

Площадь поверхности сферы:

S=4πR2,

где R – радиус шара, S - площадь сферы.

Объем сферы

V =

где V – объём шара

Объем шарового сектора

V = ,

V – объём шарового сегмента.

Площадь сегментальной поверхности

где - высота сегмента, площадь сегментальной поверхности

Радиус основания сегмента

,

где - радиус основания сегмента, - высота сегмента, 0<H<2R.

Площадь сферической поверхности шарового сегмента

где - площадь сферической поверхности шарового сегмента.

В пространстве для шара и плоскости возможны три случая:

1) Если расстояние от центра шара до плоскости больше радиуса шара, то шар и плоскость не имеют общих точек.

2) Если расстояние от центра шара до плоскости равно радиусу шара, то плоскость имеет с шаром и ограничивающей его сферой только одну общую точку.

3) Если расстояние от центра шара до плоскости меньше радиуса шара, то пересечение шара с плоскостью представляет собой круг. Центр этого круга является проекцией центра шара на данную плоскость. Пересечение плоскости со сферой является окружностью указанного круга.

1.2 Описанная сфера

1.2.1 Определения и свойства

Сфера называется описанной около многогранника (а многогранник — вписанным в сферу), если все вершины многогранника лежат на сфере.

Из определения описанной сферы следуют два факта:

1) все вершины вписанного в сферу многогранника равноудалены от некоторой точки (от центра описанной сферы);

2) каждая грань вписанного в сферу многогранника является вписанным в некоторую окружность многоугольником, именно в ту окружность, которая получается в сечении сферы плоскостью грани; при этом основание перпендикуляров, опущенных из центра описанной сферы на плоскости граней, являются центрами описанных около граней окружностей.

Теорема 1. Около многогранника можно описать сферу, если и только если выполняется любое из условий:

а) около всякой грани многогранника можно описать окружность, и оси окружностей, описанных около граней многогранника, пересекаются в одной точке;

б) плоскости, перпендикулярные к ребрам многогранника и проходящие через их середины, пересекаются в одной точке;

в) существует единственная точка, равноудаленная от всех вершин многогранника.

 Скачать реферат