Описанная сфера на олимпиадах и ЕГЭ

Рефераты / Математика / Описанная сфера на олимпиадах и ЕГЭ

По условию,

R3 = V,

откуда R3 = , следовательно,

Vприз.

Ответ: Vприз.

order=0 width=178 height=172 src="images/referats/7497/image081.jpg">

Рис.17

Пример 2. Найти отношение поверхности и объёма шара соответственно к поверхности и объёму вписанного куба

Решение. Пусть радиус шара равен R, ребро куба равно а;

тогда R2 - , откуда а= .

Обозначим объемы и поверхности шара и куба соответственно через V1, V2, и S1, S2.

Имеем

V1=, V2 == , S1 =4, S2=6а2 =8R2,

откуда

V1V2 = , S1S2 = .

Ответ: V1V2 = , S1S2 = .

2.3 Примеры олимпиадных заданий с цилиндром

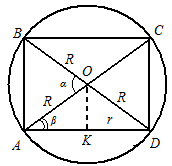
Рис.18

Пример. Найдите отношение объёма шара к объёму прямого кругового цилиндра, вписанного в этот шар, если известно, что меньший угол между диагоналями осевого сечения цилиндра равен и диаметр основания больше высоты цилиндра (рис. 18).

Решение. Объём шара нам известен , а объём цилиндра найдём по формуле , но , поэтому

Пусть ABCD - осевое сечение цилиндра (см. рис. 18). Так как диаметр основания, больше высоты цилиндра, то – угол АОВ. Из треугольника АВО следует, что высота цилиндра

Радиус основания цилиндра

Угол .

Получается, что

Подставим найденные данные в формулу объёма цилиндра:

;

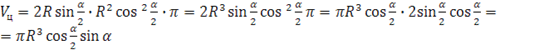Таким образом,

Найдём отношение

Ответ: .

2.4 Примеры олимпиадных заданий с конусом

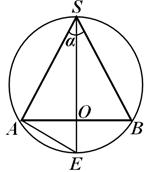
Рис.19

Пример 1. В шар радиуса R вписан круговой конус; угол между образующими конуса в осевом сечении равен α. Найти высоту, образующую и радиус основания конуса.

Решение. Сечение шара, проходящее через ось конуса,— это большой круг шара, в который вписан АВS (рис. 19), где AВ — диаметр основания конуса. Продолжим высоту (ось) конуса SO до пересечения с окружностью большого круга в точке Е и рассмотрим ЕSА:

в этом треугольнике

SE = 2R, SАЕ = 90° и АSЕ=.

Поэтому

АS = 2R.

Теперь из АOS находим

AО= r = 2R, SO = h=2R

Ответ: SO=2RАS = 2R, AО=.

Пример 2. Отношению высоты конуса к радиусуописанного вокруг него шара равно k. Найти отношение объёмов этих тел. Выяснить при каких k задача имеет смысл.

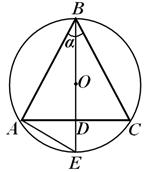
Рис.20

Решение. Рассмотрим осевое сечение конуса (рис. 20). Пусть h — высота конуса, R — радиус шара, описанного около конуса. Тогда, по условию, =k, т. е. h = kR.