Описанная сфера на олимпиадах и ЕГЭ

DM – диаметр шара. Тогда в сечении шара, проходящем через диаметр DM и точку А, получим прямоугольный треугольник AMD. Из метрических соотношений в прямоугольном треугольнике имеем ,

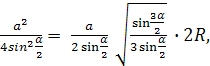откуда

Тогда площадь основания найдем по формуле:

.

И из формулы находим объем пирамиды:

.

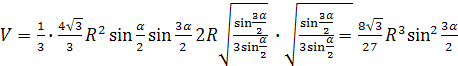Ребро AD по определению описанного конуса является его образующей. Тогда найдем боковую поверхность описанного конуса по формуле Sбок = rl:

.

Ответ: ; .

Пример 3. В основании пирамиды лежит квадрат со стороной а. Высота пирамиды проходит через середину одного из ребер основания и равна. Найти радиус сферы, описанной около пирамиды.

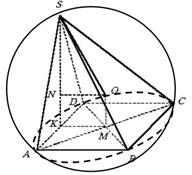
Рис.11

Решение. Типичной ошибкой при решении этой задачи является утверждение о том, что центр описанной сферы находится на грани SBC (рис. 11). В действительности положение точки О не связано с гранью SBC.

В силу равноудаленности точки О от вершин S, A, B, C, D следует, что OABCD – правильная четырехугольная пирамида. Следовательно, на грань ABCD точка О проектируется в точку М – точку пересечения диагоналей. Треугольник ASD равнобедренный, тогда высота пирамиды SK является медианой треугольника ASD, . Из прямоугольного треугольника SAK найдем SA:

,

Следовательно, треугольник SAD – равносторонний и OASD – правильная треугольная пирамида. Тогда точка О проектируется на грань SAD в центр треугольника SAD . Отсюда

, .

Из треугольника SON находим искомый радиус SO,

, .

Ответ: .

Пример 4. В шар радиуса R вписана правильная шестиугольная усечённая пирамида, у которой плоскость нижнего основания проходит через центр шара, а боковое ребро составляет с плоскостью основания угол 60. Определить объём пирамиды.

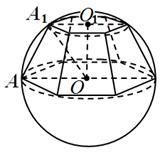
Рис.12

Решение. По условию, OAA1 = 60(рис. 12); значит,

О1ОА1=30и А1О1 = А1О = ,OO1 = .

Находим

Sнижн.осн.= 6, Sверхн. осн.=нижн. осн..

Окончательно получим

.

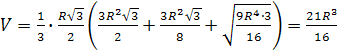Ответ:

2.2 Примеры олимпиадных заданий с призмой

Пример 1. В шар, объем которого равен V, вписана прямая треугольная призма. Основанием призмы служит прямоугольный треугольник с острым углом , а наибольшая ее боковая грань есть квадрат. Найти объем призмы.

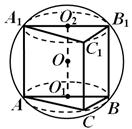
Рис.13

Решение. Сначала определим положение центра шара относительно призмы. Сечения шара плоскостями оснований призмы - круги, в которые вписаны эти основания (рис. 13), а так как основания призмы равны, то равны и одинаково удалены от центра шара круги сечений. Каждый из центров О1 и О2 совпадает с серединой соответствующей гипотенузы.

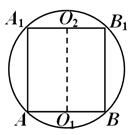
Рис.14

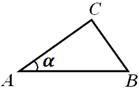
Рис.15

Из свойств сечений шара плоскостью известно, что перпендикуляр, проведенный из центра шара О к плоскости круга сечения, проходит через центр этого круга. Следовательно, О1Оплоскости АВС. Прямая О1О проходит также через O2 и перпендикулярна плоскости Таким образом, центр шара лежит на грани в середине отрезка O1O. Все боковые грани призмы — прямоугольники, причем грань — наибольшая из них (так как АВ — гипотенуза треугольника AВС). Эта грань по условию — квадрат. Сечение шара плоскостью грани — большой круг шара, поэтому радиус круга, изображенного на рис. 14, равен радиусу шара R. Заметим, что высота призмы АА1 = a4 = . Теперь остается найти площадь основания:

SАBС =. Из (рис. 15)

имеем АС = АВ, значит,

SАBС=.

Теперь получаем:

Vприз..

 Скачать реферат