Описанная сфера на олимпиадах и ЕГЭ

Рефераты / Математика / Описанная сфера на олимпиадах и ЕГЭ

Пример 3. В усеченном конусе радиусы нижнего и верхнего оснований равны соответственно r1 и r2, а образующая конуса наклонена к плоскости нижнего основания под углом α (рис. 21). Найти радиус шара, в который вписан данный усеченный конус.

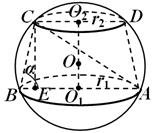
Рис.21

Решение. В сечении шара, проходящем через ос

ь усеченного конуса, получается большой круг шара, в который вписана трапеция АВСD. Рассмотрим AВС, который также вписан в большой круг шара. В этом треугольнике известен угол СBA = α. В силу теоремы синусов, АС = 2R . Таким образом, для определения R достаточно найти АС. Опустим из точки С перпендикуляр СЕ на АВ. Очевидно,

АЕ= r1 + r2, ВЕ = r1 - r2, а СЕ = (r1 - r2).

Поэтому по теореме Пифагора

АС = = =

==, откуда R= .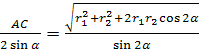

Ответ: R.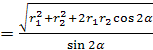

3 Примеры заданий ЕГЭ

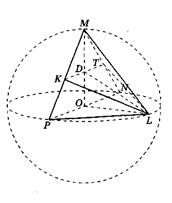
Рис. 22

3.1 Примеры заданий ЕГЭ с пирамидой

Пример 1. Отрезок РN, равный 8, — диаметр сферы. Точки М, L лежат на сфере так, что объем пирамиды РNМL наибольший (рис. 22). Найдите площадь треугольника КLТ, где К и Т — середины ребер РМ и NМ соответственно.

Решение. Пусть О — центр сферы, а R — ее радиус. Поскольку РN = 2R = 8 и точки М и L лежат на сфере, то ОР = ОL = ОN = ОМ = R = 4. Сечения сферы плоскостями РLN и РМN — окружности радиуса R = 4, описанные около треугольников РLN и РМN, причем РМN = РLN = 90°, как вписанные углы, опирающиеся на диаметр РN.

Пусть Н — высота пирамиды, опущенная из вершины М, а h — высота треугольника РLN, проведенная к стороне РN. Поскольку точка М лежит на сфере, а плоскость РLN содержит центр сферы, то Н R, причем Н = R, если МО РNL. Аналогично, так как точка L лежит на сфере, то h R, причем h= R, если LОРN.

Отсюда для объема пирамиды РNМL имеем

При этом

если .

Таким образом, пирамида РNМL имеет наибольший объем, если треугольники РLN и РМN прямоугольные, равнобедренные с общей гипотенузой РN, лежащие во взаимно перпендикулярных плоскостях. Так как треугольники LОN, LОР, LОМ, РОМ, NОМ равны по двум катетам, то треугольники LМN и LМР правильные со стороной

NL=РL=ON=4

Отсюда следует, что медианы LК и LТ этих треугольников равны, причем

LК = = 2.

Треугольник КLТ равнобедренный, и его высота LD является медианой прямоугольного равнобедренного треугольника LОМ. Отсюда

LD = =2.

КТ — средняя линия треугольника РМN и поэтому КТ = 0,5РN =R. Следовательно, площадь SКLТ = КТLD = 4.

Ответ: 4.

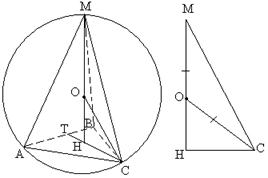
Рис.23

Пример 2. В правильной треугольной пирамиде сторона основания равна 5, а боковые рёбра наклонены к основанию под углом 60о. Найдите радиус, описанной вокруг пирамиды сферы.

Решение. Пусть АВСМ указанная пирамида (см. рис. 23) Центр описанной сферы лежит на высоте пирамиды, т. к. пирамида правильная.

Основание высоты пирамиды – центр треугольника АВС, т. е. точка пересечения медиан. Тогда:

СН= СТ = СН= = =.

Теперь рассмотрим треугольник МНС. Здесь угол МСН равен 60о, как угол между боковым ребром МС и основанием АВС. Угол НМС равен 30. МО=ОС как радиусы. Значит, треугольник МОСравнобедренный. Как известно, в равнобедренном треугольнике углы при основании равны. Следовательно,