Некоторые приложения дифференциального исчисления
Если перейти к прямоугольным координатам, взяв полюс за начало, а полярную ось - за ось х, то уравнения
x = r cos![]() =f(
=f(![]() ) cos
) cos![]() , у=rsin
, у=rsin![]() =f(
=f(th=13 height=19 src="images/referats/663/image186.gif">)sin
![]()
дадут параметрическое представление нашей кривой, причем роль параметра здесь будет играть полярный угол![]() .
.
Формулы: ![]()
Показывают, что особая точка может встретится лишь в том случае, если ![]()
Длина плоской кривой
Пусть имеем (незамкнутую или замкнутую) плоскую кривую АВ, заданную параметрически уравнениями:
![]() ,
,
где функции ![]() и
и ![]() здесь предполагаются непрерывными. Пусть кратных точек на кривой нет, так что каждая точка получается лишь при одном значении параметра t. При этих предположениях кривую будем называть непрерывной простой кривой.
здесь предполагаются непрерывными. Пусть кратных точек на кривой нет, так что каждая точка получается лишь при одном значении параметра t. При этих предположениях кривую будем называть непрерывной простой кривой.
Точка А отвечает значению параметра t=t0, а точка B-значению t=T. Точка А называется начальной, а точка B конечной точкой кривой. Из двух отличных от A и B та считается следующей, которая отвечает большему значению параметра.
Возьмем на кривой ряд точек: А = М0, М1 ,М2 , ., Мi ,Mi+1,…, Мn = В так, чтобы они шли в указанном возрастающим значениям параметра t0 <t1<t2<…<ti<ti+1<…<tn.
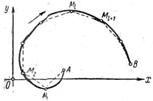
Рис. 16
Соединяя эти точки последовательно прямолинейными отрезками (рис. 16), мы получим ломаную М0М1 . Мn-1 Мn вписанную в кривую АВ.
Длиной кривой АВ, называется точная верхняя граница S для множества периметров р всевозможных вписанных в кривую ломаных: S=Sup{p}.
Если это число S конечно, то кривая называется спрямляемой.
Пусть функции ![]() и
и ![]() имеют непрерывные производные
имеют непрерывные производные ![]() и
и ![]() на
на ![]() . Тогда длина дуги вычисляется по формуле
. Тогда длина дуги вычисляется по формуле 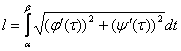 или
или ![]() (1)
(1)
Если кривая задана полярным уравнением r = g(![]() ), то это равносильно заданию ее параметрическими уравнениями
), то это равносильно заданию ее параметрическими уравнениями
х = r cos![]() , у = rsin
, у = rsin![]() ,
,
где параметр - ![]() ; дуга будет функцией от
; дуга будет функцией от![]() : s = s(
: s = s(![]() ). Так как
). Так как
![]()
То ![]()
и формула (1) примет вид:
![]()
Кривизна плоской кривой.
Пусть дана простая кривая x = ![]() (t), y =
(t), y = ![]() (t) (t0
(t) (t0![]() ) , (1)
) , (1)
где функции ![]() и
и ![]() предполагаются непрерывными вместе со своими производными первого и второго порядка.
предполагаются непрерывными вместе со своими производными первого и второго порядка.
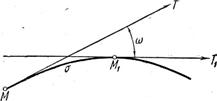
Рис. 17
Пусть ![]() , есть дуга кривой; рассмотрим касательные МТ и M1T1 проведенные в конечных точках этой дуги. Кривизну кривой будем характеризовать углом поворота касательной, рассчитанным на единицу длины дуги, т.е. отношением
, есть дуга кривой; рассмотрим касательные МТ и M1T1 проведенные в конечных точках этой дуги. Кривизну кривой будем характеризовать углом поворота касательной, рассчитанным на единицу длины дуги, т.е. отношением ![]() , где угол
, где угол ![]() измеряется в радианах, а длина
измеряется в радианах, а длина ![]() - в выбранных единицах длины. Это отношение называют средней кривизной дуги кривой.
- в выбранных единицах длины. Это отношение называют средней кривизной дуги кривой.
Кривизной кривой в точке М называется предел, к которому стремится средняя кривизна дуги MM1 ,когда точка М1 вдоль по кривой стремится к М.
Кривизну кривой в данной точке обозначаем буквой k:
![]()
Возьмем на участке кривой точку М, и пусть ей отвечает значение s дуги. Придав s произвольное приращение ![]() , получим другую точку
, получим другую точку ![]() (рис. 18). Приращение
(рис. 18). Приращение ![]() угла наклона касательной при переходе от М к М1 даст угол
угла наклона касательной при переходе от М к М1 даст угол ![]() между обеими касательными:
между обеими касательными: ![]()
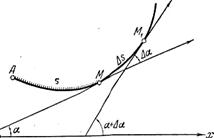
Рис. 18
Так как![]() , то средняя кривизна будет равна
, то средняя кривизна будет равна ![]()
Устремив MM1 =![]() к нулю, получим выражение для кривизны кривой в точке М:
к нулю, получим выражение для кривизны кривой в точке М:
![]() (2)
(2)
Перепишем формулу (2) иначе:
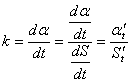 (3)
(3)
![]() . Нужно найти
. Нужно найти ![]() . Так как
. Так как
![]() и
и ![]() , то
, то

Подставив в (3) значения ![]() и
и ![]() получим конечную формулу:
получим конечную формулу:
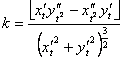 (4)
(4)
Если кривая задана явным уравнением y=f(x), то эта формула принимает вид:
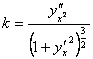
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
