Некоторые приложения дифференциального исчисления
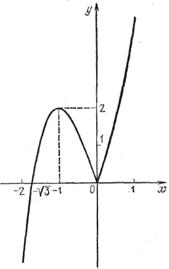
Рис. 8
Решение
Запишем функцию двумя разными формулами для промежутков ( 6) Миноносец стоит на якоре в 9 км. От ближайшей точки берега; с миноносца нужно послать гонца в лагерь, расположенный в 15 км., считая по берегу от ближайшей к миноносцу точки берега (лагерь расположен на берегу). Если гонец может делать пешком по 5 км/ч, а на вёслах 4 км/ч, то в каком пункте берега он должен пристать, чтобы попасть в лагерь в кратчайшее время?
Решение
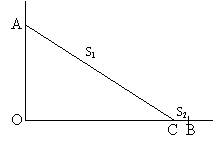
Рис. 9
OA=9 км (рис. 9)
OB=15 км
Пусть S1 гонец проплывает со скоростью v1=4 км/ч, а путь S2 гонец проходит со скоростью v2=5 км/ч. Пусть OC=x, тогда Тогда исследуемая функция будет выглядеть:
Дифференцируя полученную функцию имеем:
Получаем x = 12 (км). Знак первой производной для значений, несколько меньших 12 и несколько больших 12 меняется с “-” на ”+”, т.е. функция t при x = 12 имеет минимум. Гонец должен доплыть до пункта C, находящемуся на расстоянии 12 км. от пункта O.
Производные высших порядков
Наряду с производной Производная от второй производной называется третьей производной или производной третьего порядка; производная от третьей производной - производной четвертого порядка и т.д. Производная порядка п от функции f (х) обозначается f(n) (х).
Первая производная Рис. 10
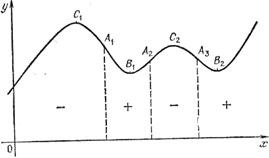
Вторая производная есть скорость изменения углового коэффициента касательной. Положительность второй производной на некотором интервале означает, что угол, образованный касательной с осью абсцисс, растет с увеличением x. Геометрически это значит, что график направлен выпуклостью вниз. Если же вторая производная отрицательна на некотором интервале, то на нем график расположен выпуклостью вверх. На рис. 4 интервал задания функции разбит на участки, на каждом из которых вторая производная сохраняет знак (этот знак указан на рисунке). Точки, в которых график меняет направление выпуклости, называются точками перегиба. точки А1, А2, А3 на рис. 4). При переходе через точку перегиба вторая производная меняет знак.
Наглядно видно, что если в некоторой точке первая производная равна нулю, а вторая положительна (точки В1 и В2 на рис. 4), то в этой точке функция имеет минимум, так как в такой точке касательная к графику горизонтальна и выпуклость направлена вниз. Соответственно если первая производная в точке равна нулю, а вторая отрицательна, то в этой точке имеет место максимум (точки С1 и С2 на рис. 4).
Если Предположим, что функция f(x) имеет в точке х =x0 n последовательных производных, причем все они, вплоть до (n-1) в этой точке обращаются в нуль:
но Так к все производные порядков меньших, чем n, равны в точке х0 нулю, то
Так как 1) n - нечетное число: n = 2k+1. При переходе от значений x к x0, меньших, чем х0, к значениям, большим, чем х0, выражение (х – х0)n изменит знак на обратный, а так как знак первого множителя при этом не меняется, то и знак разнести f(x)-f(x0) изменится. Таким образом, в точке х0 функция f(x) не может иметь экстремума, потому что вблизи этой точки принимает значения как меньше, так и большие, чем f(х0).
![]() ;0) и [0; +
;0) и [0; +![]() ). На первом промежутке
). На первом промежутке ![]() , на втором
, на втором ![]() < x < 0 имеем
< x < 0 имеем ![]() . Производная обращается в нуль при х = 1 и х = -1. Первая из этих точек не принадлежит промежутку (
. Производная обращается в нуль при х = 1 и х = -1. Первая из этих точек не принадлежит промежутку (![]() ; 0). На промежутке (
; 0). На промежутке (![]() ; - 1) производная положительна, на промежутке (- 1; 0)- отрицательна, поэтому -1 -точка максимума. На промежутке (0;
; - 1) производная положительна, на промежутке (- 1; 0)- отрицательна, поэтому -1 -точка максимума. На промежутке (0; ![]() ) производная у'= Зх2 + 3 > 0, значит функция возрастает на промежутке, и точка x = 0, в которой производная от функции
) производная у'= Зх2 + 3 > 0, значит функция возрастает на промежутке, и точка x = 0, в которой производная от функции ![]() не существует, оказывается точкой минимума. График имеет вид, изображенный на рис. 8.
не существует, оказывается точкой минимума. График имеет вид, изображенный на рис. 8.
![]() км/ч
км/ч
![]() 5 км/ч
5 км/ч
![]()
![]()
![]()
![]()
![]()
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]() функции f(x) часто возникает потребность в рассмотрении производной
функции f(x) часто возникает потребность в рассмотрении производной ![]() функции
функции ![]() . Она называется второй производной функции f(x). Производная есть скорость изменения функции. Поэтому вторая производная есть скорость изменения скорости изменения функции или, вторая производная есть ускорение изменения функции.
. Она называется второй производной функции f(x). Производная есть скорость изменения функции. Поэтому вторая производная есть скорость изменения скорости изменения функции или, вторая производная есть ускорение изменения функции.
![]() функции f(x) имеет ясный геометрический смысл. Она есть угловой коэффициент касательной, т.е. равна тангенсу угла наклона касательной коси абсцисс (рис. 10).
функции f(x) имеет ясный геометрический смысл. Она есть угловой коэффициент касательной, т.е. равна тангенсу угла наклона касательной коси абсцисс (рис. 10).
![]() = 0 и
= 0 и ![]() , то функция f(x) достигает в точке х0 минимума; если же
, то функция f(x) достигает в точке х0 минимума; если же ![]() = 0 и f"(x0)<0, то функция имеет в этой точке максимум. Рассмотрим случай, когда и
= 0 и f"(x0)<0, то функция имеет в этой точке максимум. Рассмотрим случай, когда и ![]() = 0 и f//(х0) = 0,
= 0 и f//(х0) = 0,
![]()
![]() . Разложим приращение f{x)-f(x0) функции f(x) по степеням разности х - х0 по формуле Тейлора с дополнительным членом в форме Пеано.
. Разложим приращение f{x)-f(x0) функции f(x) по степеням разности х - х0 по формуле Тейлора с дополнительным членом в форме Пеано.
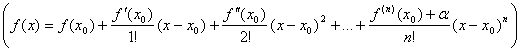
![]()
![]() при
при ![]() , при достаточной близости x к х0 знак суммы в числителе будет совпадать со знаком f{n) (x0) как для х<х0, так и для x>x0. Рассмотрим два случая:
, при достаточной близости x к х0 знак суммы в числителе будет совпадать со знаком f{n) (x0) как для х<х0, так и для x>x0. Рассмотрим два случая:
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
