Некоторые приложения дифференциального исчисления

На рис. 4 точка х0 - точка локального минимума функции f(x), x1 есть точка локального максимума. Глобальные минимум и максимум достигаются на концах а и b промежутка задания функции.

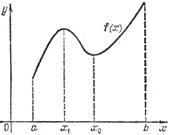
Рис. 4

Максимум и минимум функции носят общее название экстремумов, и точки, в которых они достигаются, называются точками экст

ремумов.

Рассмотрим задачу, в которой нужно найти все значения аргумента, доставляющих функции экстремум.

Точка локального максимума - точка х0, для которой f(x0) - наибольшее среди всех значений в некоторой окрестности точки х0. Локальный максимум функции - значение f(x0) в точке локального максимума, глобальный максимум - наибольшее значение функции, заданной на интервале. Точка х0 называется точкой локального минимума для функции f(x), если ее значение f(x0) в этой точке меньше всех значений в некоторой ее окрестности , то есть . Значение f(x0) называется локальным минимумом функции f(x). Глобальным (всеобщим) минимумом называется значение функции, наименьшее среди значений на всем интервале.

Максимум и минимум функций

Если функция f(x), определенная и непрерывная в промежутке [а, b], не является в нем монотонной, то найдутся такие части промежутка [а, b], в которых наибольшее или наименьшее значение достигается функцией во внутренней точке.

Точка х0 называется точкой локального минимума для функции f(x), если ее значение f(x0) в этой точке меньше всех значений в некоторой ее окрестности , то есть . Значение f(x0) называется локальным минимумом функции f(x). Глобальным (всеобщим) минимумом называется значение функции, наименьшее среди значений на всем интервале.

Точка локального максимума - точка х0, для которой f(x0) - наибольшее среди всех значений в некоторой окрестности точки х0. Локальный максимум функции - значение f(x0) в точке локального максимума, глобальный максимум - наибольшее значение функции, заданной на интервале.

На рис. 5 точка х0 - точка локального минимума функции f(x), x1 есть точка локального максимума. Глобальные минимум и максимум достигаются на концах а и b промежутка задания функции.

Рис. 5

Максимум и минимум функции носят общее название экстремумов, и точки, в которых они достигаются, называются точками экстремумов.

Рассмотрим задачу, в которой нужно найти все значения аргумента, доставляющих функции экстремум.

Предположим, что для функции f(x) в промежутке (a.b) существует конечная производная. Если в точке x0 функция имеет экстремум, то применив к промежутку теорему Ферма (пусть функция f(x) определена в некотором промежутке и во внутренней точке с этого промежутка принимает наибольшее (наименьшее) значение. Если существует двусторонняя конечная производная в этой точке, то необходимо ), получим, что : в этом состоит необходимое условие экстремума. Экстремум нужно искать только в тех случаях, где производная равна 0. Эти точки называются стационарными.

Не каждая стационарная точка доставляет функции экстремум: необходимое условие не является достаточным. Например, для функции производная обращается в нуль при x=0, но в этой точке функция не имеет экстремума: она всё время возрастает.

Если точка - стационарная точка для функции f(x) или если в этой точке не существует для нее двусторонней конечной производной, то точка х0 является лишь «подозрительной» по экстремуму и подлежит проверке достаточных условий для существования экстремума.

Первое правило для испытания “подозрительного” значения х0: подставляя в производную сначала х<х0, а затем x>x0, устанавливаем знак производной вблизи от точки х0 слева и справа от нее; если при этом производная меняет знак плюс на минус, то имеем максимум, если меняет знак минус на плюс, то - минимум; если же знака не меняет, то экстремума нет.

Это правило решает вопрос в том случае, когда в промежутке (а,b), всего лишь конечное число стационарных точек или точек, где отсутствует конечная производная:

(1)

Тогда в любом промежутке

существует конечная производная и в каждом таком промежутке сохраняет постоянный знак. Если бы меняла знак, например, в промежутке (xk ,xk+1), то, по теореме Дарбу (Если функция f(x) имеет конечную производную в промежутке [a,b], то функцияпринимает, в качестве значения, каждое промежуточное число между и ), она обращалась бы в нуль в некоторой точке между xk и xk+1, что невозможно, поскольку все корни производной уже содержатся в ряду точек (1). Последнее замечание применимо в некоторых случаях на практике: знак производной во всем промежутке (xk,,хk+1) определится, если вычислить значение (или даже только установить знак) ее в одной какой-либо точке этого промежутка.

При разыскании экстремумов исследование знака производной вблизи испытуемой точки можно заменить исследованием знака второй производной в самой этой точке.

Пусть функция f(x) имеет производную f (x) в окрестности точки х0, и вторую производную в самой точке х0:. Точка х0 - стационарная, т.е.. Если , то функция в точке х = х0 возрастает, т.е. вблизи точки х0 слева , а справа . Таким образом, производная меняет знак минус на плюс и, следовательно, f(x) имеет в точке х=х0 минимум. Если, f"(x0)<0, то в точке х = хо убывает, меняя знак плюс на минус, то имеем максимум.

 Скачать реферат