Некоторые приложения дифференциального исчисления

2) n - четное число: n = 2k. В этом случае разность f(x) – f(x0) не меняет знака при переходе от х меньших, чем х0, к большим, так как (х – х0)n>0 при всех х. Очевидно, вблизи х0 как слева, так и справа знак разнести f(x)-f(х0) совпадает со знаком числа f{n) (х0). Значит, если , то f(x)>f(x0) вблизи точки х0, и в точке х0 функ

ция f(x) имеет минимум; если же f{n)(х0)<0, то функция имеет максим.

Теорема. Пусть функция f(x), заданная на интервале [а, b], имеет производные и в некоторой точке [а,b] имеет место f'{c)= .

Тогда если f(n){x) > 0 при всех х[а, b], то при четном n функция f(x) имеет минимум при х = с, если же нечетно, то функция f(x) возрастает на [а, b] и для нее х = с-точка перегиба. Соответственно если f(n)(x)<0 при всех х[а, b], то при четном n функция f(x) имеет максимум в точке х = с, а при нечетном функция f(x) убывает на [а, b] и для нее х = с-точка перегиба.

Рис. 11

Доказательство. Пусть условия теоремы выполнены и f(n) (х) > 0 (рис. 5). Тогда f{n-1)(x) возрастает в интервале [а, b], так что при х < с будет (рис. 11) и при х >c: (рис. 12).

Рис. 12

Рис. 13 Рис. 14

Таким образом, f{n-l)(x) отрицательна при х<c и f(n-1)(x) положительна при x>с. Следовательно, f{n-2)(x) убывает слева от точки х = с и возрастает справа от точки х = с. Она обращается в нуль при х = с.

Поэтому она принимает положительные значения как слева, так и справа от точки х = с и имеет минимум при х = с (рис. 13). Функция f{n-3) (х) возрастает слева и справа от точки x= с, так что, обращаясь в нуль при х = с, переходит от отрицательных значений к положительным (рис. 14). Функция f(n-4) (х) убывает слева отточки х = с и возрастает справа. Следовательно, она имеет минимум и равна нулю при х = с и принимает положительные значения как слева, так и справа от с. Продолжая аналогичные рассуждения, мы получим, что f{n-1)(x), f(n-3)(x). f(n-5) (x)…. возрастают, когда х проходит через точку х = с, a f(n-2)(x), f{n-4) (x), f(n-6) (x)…. имеют минимум при х = с. При четном n дойдем до исходной функции f (х) через четное число шагов, делаем вывод, что f (x) имеет минимум при х = с. При нечетном n мы дойдем до f(x) за нечетное число шагов и заключим, что f (x) возрастает слева от точки х = с и продолжает возрастать справа от нее. f" (x) тоже возрастает, проходя через нулевое значение, и, следовательно, f" (х) меняет знак с минуса на плюс, значит, точка с есть точка перегиба для функции f(x).

Случай f{n) (x) < 0 рассматривается аналогично. Теорема доказана.

Если функция задана параметрические: и , то производные вычисляются по формулам:

; ; ,….

Производную второго порядка можно вычислить по формуле:

Примеры

1) . Найти

2) Найти , , если

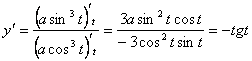
3) При помощи производных высших порядков исследовать функцию f(х) = х5-2x4 + х3 + 2 на максимум и минимум (рис. 15).

Решение.

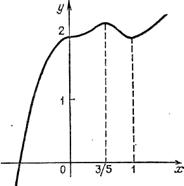
Рис. 15

(x)== 5x4 – 8x3 + 3x2 = x2(5х2-8x+3). Корни производной: х1 = 0; х2 = 3/5; х3=1. Имеются три «подозрительные» точки. Вторая производная

f" (x) = 20x3 - 24x2 + 6x, = 0;

Точка x = 3/5 есть точка максимума, х = 1 - точка минимума. Далее: f"' (х) = 60х2-48х+6; f'" (0) = 6 > 0.

Следовательно, точка х = 0 есть точка перегиба на возрастании. График имеет вид, представленный на рис. 15.

Формулы Тейлора и Маклорена

Для функции f(х), имеющей n+1 непрерывных производных в окрестности точки х = а, всегда можно найти многочлен Рn(х) степени n такой, чтобы он имел порядок близости к f (х) не менее n+1 в окрестности точки х = а. Докажем это.

Пусть Рn (х) == а0 + а1х + а2х2 + . + аnхn, есть целый многочлен степени n. Запишем х = (х-а) + а и преобразуем степени х по формуле бинома Ньютона. Каждое слагаемое akxk представится в виде суммы степеней двучлена (х-а) с некоторыми коэффициентами. Соединив подобные члены, представим Рn(х) в виде

Pn(x) = b0 + bl{x-a) + b2(x-a)2+…+bn{x-a)n.

В этой форме будем искать Рn{х).

Пусть rn(х) = f (х)-Рn(х)=f(х)-b0-b1(х-а) - b2(х-а)2-….- bk(x-a)k- . – bn(x - a)n. Необходимо, чтобы

rn(а) = r'n(а)= .=r(n)(a)=0. Вычислим производные от функции rn(х):

Приравняв к нулю получим:

f(a)-b0=0; ;….,откуда

b0=f(a),

При таком выборе коэффициентов функция rn(x) будет иметь порядок малости не меньше n+1 и соответственно Р(х) будет иметь порядок близости к f(x) не меньше n+1.

 Скачать реферат