Некоторые приложения дифференциального исчисления

Второе правило для испытания «подозрительного» значения х0: подставляем х0 во вторую производную :если , то функция имеет минимум, если же f" (х0) < 0, то - максимум.

Это правило имеет ограничение в применении: оно неприложимо к тем точкам, где не существует

конечной первой производной; когда вторая производная обращается в нуль, правило также ничего не дает. Решение вопроса зависит тогда от поведения высших производных.

Замечание. При решении задач практического содержания часто можно не проверять аналитически достаточность условий экстремума (с помощью первой или второй производной). Заключение о наличии экстремума обычно легко сделать на основании условий задачи. Это относится также и к отысканию наибольших и наименьших значений.

План решения текстовых задач на экстремум:

1. Выбрать независимую переменную и установить область её применения.

2. Выразить исследуемую величину через аргумент.

3. Найти стационарные точки и точки, в которых исследуемая функция не имеет производной (в частности, точки, где производная обращается в бесконечность). Из числа последних точек исключить точки несуществования функции.

4. Вычислить значения функции в найденных точках и на концах отрезка изменения аргумента и выбрать из этих значений наибольшее или наименьшее.

Примеры.

1) Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трёх сторон она была огорожена проволочной сеткой, а четвёртой стороной примыкала к стене. Для этого имеется a погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?

Решение

Обозначим стороны площадки x и y. Площадь площадки равна S=xy. По условию, данному в задаче, должно выполняться равенство . Поэтому и , где . (Потому что длина и ширина площадки не могут быть отрицательными).

, , ,

Так как , то при функция S имеет максимум. Значение функции

S =кв. ед.

Так как функция S(x) непрерывна на и её значения на концах S(0) и S() равны нулю, то найденное значение будет наибольшим значением функции. Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является

2) В данный шар вписать цилиндр, имеющий наибольшую боковую поверхность (рис. 6).

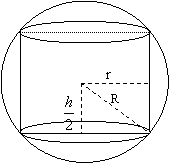
Рис. 6

Пусть радиус шара R, а радиус основания цилиндра r. Тогда высота цилиндра h определится по формуле , а боковая поверхность , при этом . Отсюда , при , откуда

Функция S(r) положительна и непрерывна на . На концах отрезка она равна нулю. Следовательно, внутри отрезка при она имеет наибольшее значение. Цилиндр такого радиуса будет искомым.

3) Найти стороны прямоугольника наибольшего периметра, вписанного в полуокружность радиуса R.

Решение

Обозначим стороны прямоугольника через x и y. Тогда периметр равен . Выразим y через x, зная, что радиус полукруга R (из прямоугольного треугольника):

, .

Тогда периметр

Находим производную:

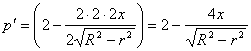, при этом

при

Таким образом, прямоугольник должен иметь стороны ;

4) Вокруг полушара радиуса описать прямой круговой конус наименьшего объема; при этом предполагается, что основания полушара и конуса лежат в одной плоскости и концентричны (рис. 7).

Решение

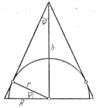
Рис. 7

Обозначим угол при вершине конуса через . Тогда получается:

И объем конуса:

Для того чтобы объем V имел наименьшее значение, очевидно, нужно, чтобы выражение у = cos2sin, стоящее в знаменателе, получило свое наибольшее значение, при изменении в промежутке . Имеем

между 0 и производная обращается в нуль при tg = , , меняя при этом знак плюс на минус. Этот угол доставляет выражению y наибольшее значение, а объёму V – наименьшее.

5) Найти для функции точки максимума, минимума, промежутки возрастания и убывания.

 Скачать реферат