Логические задачи и методы их решения

Рис. 29.

Задача 12. Три рыцаря, каждый в сопровождении оруженосца, съехались на берегу реки и хотят переправиться на другой берег. Есть лодка, которая может вместить только двух человек. Могут ли переправиться рыцари и их оруженосцы на другой берег при условии, что, оказавшись отдельно от своего рыцаря, ни один оруженосец, не находился бы при этом в обществе других рыцарей?

Такую зада

чу могут решить учащиеся 6-го класса. Передвигаяя фигурки, можно проверять и пробовать множество вариантов, при этом необходимо записывать ход решения при помощи таблиц, либо при помощи графов.

Решение: этой задачи может быть таким: А, В, С – обозначим рыцарей; а, в, с – их оруженосцев.

А В С А В С . А В С А В С .

а в с . а в с а в . с а в с

А В С в с А В С А В С А В С

а . а в с . а в . с а в с .

. А В С А В С . А В С А В С

а в с а в с . а в с а в с

Ребятам постарше можно предложить следующую задачу. Отличается от предыдущей она только условием, решение же аналогично.

Задача 13. По обычаю одной восточной страны, жене запрещается оставаться без мужа в обществе мужчин, однажды трем супружеским парам понадобилось перебраться на южный берег реки с северного. Единственное подручное средство – лодка, вмещающая двух человек. В какой последовательности они должны были переправиться, чтобы соблюсти строгий обычай?

Такова же схема решения задач на переливание жидкости. Решая такие задачи, школьники учатся планировать свои действия, запоминать ход рассуждений. Эти задачи способствуют развитию настойчивости и сообразительности, развивают аналитическое мышление.

Задача 14. Три сосуда, вместимостью 8, 5, 3 л. стоят на полке. Первый сосуд наполнен водой, а два других пусты. Как с помощью этих сосудов отмерить один литр воды? Как отмерить 4 л. воды?

Решение. Сразу встает вопрос: с чего начать? Имеющиеся сосуды могут предложить два варианта: либо из восьмилитрового сосуда наполним пятилитровый, либо трехлитровый. Нужно учесть, что вода из этих трех сосудов никуда не выливается. Это сокращает число возможных ходов.

Первый способ.

I сосуд (8 л.) 8 3 3 6 6 (1) 1

II сосуд (5л.) 0 5 2 2 0 5 (4)

III сосуд (3л.) 0 0 3 0 2 2 3

Второй способ.

I сосуд (8 л.) 8 5 5 2 2 7 7 (4)

II сосуд (5л.) 0 0 3 3 5 0 1 1

III сосуд (3л.) 0 3 0 3 (1) 1 0 3

Задача 15. Али-Баба хочет попасть в пещеру с сокровищами. Перед пещерой стоит бочка, в крышке которой имеются четыре отверстия, образующие квадрат. Под отверстиями находится по кувшину, в каждом из которых торчит селедка, хвостом вверх или вниз. Али-Баба может просунуть руки в любые два отверстия и определить расположение находящихся под ними селедок, а также повернуть одну или две по своему усмотрению. Если хвосты всех селедок окажутся направленными в одну сторону, то дверь пещеры открывается. После того, как Али-Баба вытащит руки из отверстий, бочка быстро поворачивается и останавливается, причем Али-Баба не в состоянии определить новое соотношение бочки по отношению к старому. Существует ли способ действий, позволяющий Али-Бабе за несколько попыток наверняка открыть дверь?

Решение. Для решения необходимо рассмотреть все возможные действия Али-Бабы. Например, по схеме на рисунке 31. Таким образом самое большое после пяти «ходов» Али-Баба сможет попасть в пещеру с сокровищами. Если досконально рассматривать все возможности, то на третьем шаге Али-Баба может просунуть руки в отверстия, стоящие рядом, но это усложнит его дальнейшие действия.

Рассмотрим этот вариант (рис. 30):

Во втором случае – поменяв положение одной селедки, нельзя точно знать, какая из двух комбинаций а) или б) получилась. Следующий ход делается по диагонали. В случае а) нужно изменить положение двух селедок по диагонали и дверь откроется; в случае б) этот «ход» лишний, с его помощью можно определить положение селедок.

Дальше решение идет, как в общем случае, но Али-Баба сделает на один «ход» больше. Нужно сказать, что данная задача довольно сложная. Разбирая ее решение, нужно рассуждать последовательно и доказательно, отвечая на вопросы: «А почему именно так?», «А что будет если…?». На, а потом не трудно выбрать оптимальное решение, т.е самый кортокий путь к решению задачи (рис. 31).

1.3 Задачи на нахождение пересечения или объединение множеств (круги Эйлера)

Ещё один тип задач – задачи, в которых требуется найти некоторое пересечение множеств или их объеденение, соблюдая условия задачи.

Задача 16. В шахматном турнире учавствовало 7 человек . каждый с каждым сыграл по одной партии. Сколько партий они сыграли?

Решение. При решении этой задачи в счете возможны ошибки, т.е. некоторые партии считаются дважды. Предложите ребятам найти ответ с помощью графов, обозначая каждого ученика точкой, а игры – стрелками. Остается только подсчитать стрелки (рис. 32).

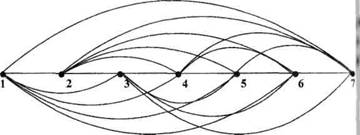
Рис. 32.

Можно оформить задачу в виде турнирной таблицы и подсчитать ее клеточки. Такие методы помогут ребятам объяснить числовое решение задачи:

Число партий =(7*6)/2=21

В дальнейшем школьники легко смогут решать такие задачи и без помощи грофов.

Задача 17. Каждые два из двадцати городов соединены линией воздушного беспересадочного сообщения. Сколько всего воздушных сообщений?

Ответ: 190

Задача 18. В учительской комнате в одну из перемен завязался разговор о журналах. В ходе его выяснилось, что каждый из учителей выписывает два журнала. На каждый из выписываемых журналов подписывается трое. Любая комбинация из двух таких журналов выписывается одним учителем сколько было учителей? Сколько было журналов выписано? Сколько номеров журналов они получили за год, если все журналы были ежемесячными?

Решение заключается в правильном построении графической схемы. Обозначим журналы точками. Каждому журналу соответствует три подписчика, т.е. из каждой точки выходят три ребра, каждое ребро соединяется еще с одной точкой (рис. 33). Каждая пара из полученных трех точек должна быть соединена отрезком. После проведения этих отрезков убеждаемся, что к графу нечего добавить.

Посмотрев на схему, можно сказать, что журналов было четыре, а учителей 6. число журналов в год легко посчитать: 6*2 *12 = 144. Или 4*3*12= 144.

При решении некоторых задач требуются более сложные построения. Пусть ребята придут к ним сами, пусть попробуют использовать уже знакомые им методы.

Еще один метод решения теоретико-множественных задач, с которыми следует познакомит ребят – это круги Эйлера.

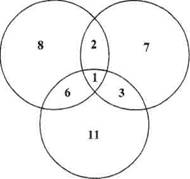
Задача 19. В школе зимой работали 3 секции (лыжная, хоккейная, конькобежная). Всего в секциях занималось 38 учеников. В лыжной - 21 человек, среди которых трое еще занимались коньками, шестеро - еще в хоккейной секции, а один - сразу в трех секциях. В конькобежной секции было 13 человек, среди которых пятеро занимались сразу в двух секциях. Сколько человек заномалось в хоккейной секции?

хоккей коньки

 Скачать реферат