Логические задачи и методы их решения

Рис.9.

Второй способ решения (рис.10).

Черная белая зеленая красная синяя

Черный

Черный белый зеленый красный синий

Красный и зеленый шарики, по условию 3, образуют пару одной коробочки. Так как в синей коробочке одно «место» занято, то эта пара может лежать тол

ько в белой. Сузим информацию. По условию 5, синий и белый шарики образуют пару. Эта пара может лежать только в зеленой коробочке (рис.11).

Черная зеленая красная синяя

Черный

Черный белый белый зеленый красный синий синий

Рис. 11.

Ещё «сузив» информацию, получим окончательное решение этой задачи (рис. 12).

Черная красная синяя

Черный

Синий белый белый черный красный

Рис. 12.

в) Сопоставление трех множеств

следующая задача «трехмерна», т.е. для ее решения нужно сопоставить три множества. Рассмотрим способ решения этой задачи при помощи таблиц.

Задача 6. «Трамвай в часы «пик».

Один психолог решил заняться изучением того, как влияет на нервную систему человека поездка в переполненном трамвае, в часы «пик». Для этого опросил по одному пассажиру с каждого из четырех маршрутов трамвая; 55, 15, 25 и 33. среди опрошенных, которых звали Андрей (А), Петр (П), Владимир (В), Леонид (Л), оказалось по одному представителю четырех профессий :слесарь(с), электромонтер (э), маляр (м), фрезеровщик (ф). К сожалению, поездки в набитых трамваях основательно истрепали нервы самому психологу. Не удивительно, что он забыл, у кого из опрошенных какая профессия. Впрочем, такая забывчивость сама по себе достаточно красноречиво говорит о том, как влияет на нервную систему человека поездка в переполненном трамвае! В памяти нашего психолога сохранились лишь бессвязные отрывки из того, что рассказывал каждый из опрошенных о своем маршруте. Разумеется, полагаться на память было нельзя, и психилог решил проверить все самым тщательным образом. Ну и, конечно, нужно было выяснить, у кого какая профессия. Вот что удалось выяснить;

1) Номер трамвайного маршрута, которым следовал Владимир, начинается не с единицы.

2) О тридцать третьем маршруте рассказывал кто-то из рабочих- металлистов.

3) Номер трамвайного маршрута, которым следовал фрезеровщик, составлен из таких цифр, что их сумма равна числу букв в имени фрезеровщика.

4) Леонид рассказал о трамвайном маршруте, номер которого состоит из двух одинаковых цифр.

5) Имя электромонтера начинается не с буквы В.

6) Петр спросил у психолога, где лучше сойти, чтобы пересесть на двадцать пятый маршрут.

7) В памяти психолога вдруг отчетливо всплыла фраза, сказанная Леонидом кому-то из пассажиров: «Вы сели не на тот трамвай, вам нужно пересесть на пятьдесят пятый».

Определите имя и профессию каждого пассажира, а также номер маршрута, о котором он рассказывал психологу.

Решение. Чтобы отразить соответствие между двумя любыми множествами, необходимо составить три таблицы. Разложив, условия задачи на элементарные запреты, отметив их в таблице, затемнив соответствующую клетку (рис. 13).

В таблице 1 (рис. 13) сразу находится частичное решение: Леонид ехал в трамвае с номером 33. Значит, что ни электромонтер, ни маляр не были пассажирами трамвая 33, и то, что Леонид не фрезеровщик, делаем вывод, что Леонид – слесарь.

На самом деле мы воспользовались «правилом треугольника». Треугольником, в данном случае, называются фигуры из трех клеток, соединенных линиями соответствия (рис. 14).

Если условия задачи непротиворечивы, то соответствующей ей схеме размещения трёх таблиц возможны лишь такие треугольники, у которых:

а) во всех вершинах расположены элементарные запреты;

б) в двух вершинах расположены элементарные запреты, а в третьей – знак соответствия (кружок);

в) во всех трех вершинах расположены знаки соответствия (кружки);

Доказательство этого правила аналогично приведенному в задаче 2. пользуясь правилом, получим окончательное решение.

Леонид - слесарь, 33-й маршрут трамвая;

Андрей - фрезеровщик, 15-й маршрут;

Владимир - маляр, 25-й маршрут;

Петр - электромонтер, 55-й маршрут трамвая.

Задачи такого типа можно давать используя только схемы расположенными на них элементарными запретами (задачи «без слов»). Кроме того, по заданной схеме учащиеся могут сами придумать условия задачи. На примере следующей задачи рассмотрим еще одно правило решения (правило переноса клеток).

Задача 7. Решите представленную на рисунке 16 задачу.

Рис. 16.

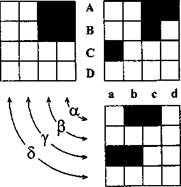
Как видно из рисунка, нельзя найти ни одного частичного решения задачи. Однако, рассмотрим на рис. 16 первую строку таблицы I. Кружок, разрешающий соответствие между элементами, может стоять либо в первой, либо во второй клетках. Предположим, что кружок стоит во 2-й клетке. Тогда клетка А-а и А-в в таблице II, по правилу треугольника, должны быть заняты элементами запрета. Первая строка в таблице II оказалась «запрещенной», но, если задача имеет решение, этого быть не может. Таким образом, кружок в таблице I, в первой строке, стоит в клетке А-б. Если посмотреть на строки А (II) и γ(III), - видно, что элементарные запреты дополняют друг друга до полной строки. Такие строки назовем дополняющими друг друга поперечными строками.

Строки (столбцы) – поперечные, если они соответствуют элементам необщих множеств. Строки таблиц, соответствующие одному и тому же элементу общего множества, назовем продольными. Они как бы служат продолжением одна другой. (Например, строка В-I и В-II, столбцы с-II, и с-III).

Теперь можно сформулировать правило переноса клеток, или правило дополнительности:

- Клетка пересечения двух дополняющих друг друга строк, являющихся поперечнымие может быть связующей клеткой ( т. е. соответствовать комбинации элементов, не запрещенной условиями задачи).

По этому правилу, поперечные, дополняющие друг друга строки А-П и γ-III пересекаются в клетке А-γ-I. Значит, в этой клетке расположен элементарный запрет, (Тот же результат был получен при помощи рассуждений). Дальше задача уже легко решается при помощи правил, известных ранее. На рисунке 17 показана клетка пересечения двух дополняющих строк.

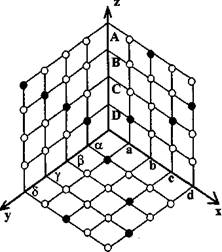
Трехмерная задача может решаться и в системе координат. Вот как выглядит такая система для данной задачи (рис.19). Все правила решения для трехмерной задачи остаются справедливыми.

 Скачать реферат