Исследование функциональных последовательностей и рядов в вузе

§8. Свойства равномерно сходящихся функциональных последовательностей и рядов

Теорема 4. Если функции непрерывны в точке и функциональный ряд равномерно сходится на множестве Х, то его сумма S (х) т

оже непрерывна в точке .

Доказательство.

Пусть - частичная сумма функционального ряда.

В соответствии с условиями теоремы, функциональный ряд равномерно сходится, значит, выполняется и равномерная сходимость последовательности частичных сумм.

На основании определения равномерной сходимости функциональной последовательности можно записать: 0 (), N,:

или .

Так как функции исследуемого ряда непрерывны в точке по условию теоремы, то частичная сумма будет непрерывна в точке , как сумма состоящая из конечного числа непрерывных функций по теореме о непрерывности функции полученной в результате алгебраического сложения и умножения двух непрерывных функций:

=++…+.

На основании определения непрерывности функции в точке на языке можно записать: 0 будет существовать такое

, , :

.

Так как последовательность функций будет равномерно сходиться к предельной функции , то и последовательность функций будет тоже равномерно сходиться к .

На основании определения равномерной сходимости функциональной последовательности можно записать: (0), (N), ():

.

Сложим три неравенства одинакового смысла пунктов 3,5,7: ++. Воспользуемся свойством модуля суммы действительных чисел , получим:

.

Следовательно, - условие непрерывности функции в точке .

Теорема доказана [14].

Замечание

1) Полученное утверждение теоремы можно переписать в следующем виде:

или ,

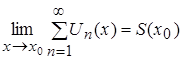так как ,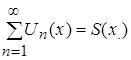

его сумма ,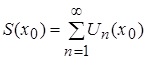

следовательно, .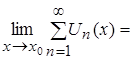

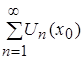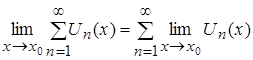2) Так как каждая функция непрерывна в точке , то для любой функции можно написать утверждение: , следовательно, . Таким образом, предел от функционального ряда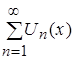равен сумме пределов его элементов [14].

Известно, что если последовательность частичных сумм функционального ряда равномерно сходится, то этот функциональный ряд тоже равномерно сходится на указанном множестве. Это обстоятельство позволяет переформулировать теорему 4 для функциональных рядов в соответствующую теорему для функциональных последовательностей.

Теорема 5. Если функции , N непрерывны в точке и равномерно сходятся к функции на множестве Х, то и функция непрерывна в точке и выполняется равенство: (предельные переходы по х и по n перестановочны).

Доказательство

Так как функции равномерно сходятся в предельной функции на множестве Х, на основании теоремы 4, то можно записать равенство: .

Функция является непрерывной в точке множества Х на основании теоремы 4. Так как непрерывна в точке , то можно записать следующее утверждение: (определение 1 непрерывности функции в точке).