Исследование функциональных последовательностей и рядов в вузе

Значит, исходный функциональный ряд сходится абсолютно на интервале , а сходится условно на полуотрезке .

Ответ: - область сходимости заданного функционального ряда.

Пример №6 (№18 из [10], студ

ент самостоятельно у доски).

Найти область сходимости функционального ряда:

Решение

По признаку Даламбера абсолютной сходимости функционального ряда можно записать:

.

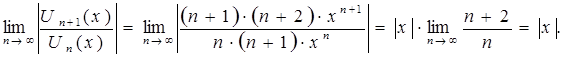Если , т.е. , то заданный функциональный ряд сходится абсолютно на интервале .

Если , т.е. , то ряд расходится.

Исследуем заданный функциональный ряд на сходимость в точках х=1 и х= - 1.

При получается числовой положительный ряд 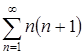. Он является расходящимся, так как не выполняется необходимое условие сходимости числового ряда, т.е. . Значит, заданный функциональный ряд в точке расходится.

При получается числовой знакочередующийся ряд вида 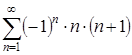. Он является расходящимся, так как не удовлетворяет условиям признака Лейбница: а) ; б) .

Ряд составленный из абсолютных величин элементов ряда имеет вид и является расходящимся.

Значит, исходный функциональный ряд расходится и в точке .

Поэтому, область сходимости заданного функционального ряда интервал - .

Ответ: .

Пример №7 (№28 из [8], студент самостоятельно у доски).

Найти область сходимости функционального ряда:

.

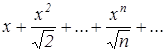Решение. Определим и заданного ряда:

, .

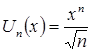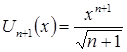По признаку Даламбера абсолютной сходимости функционального ряда имеем:

=

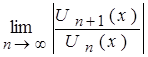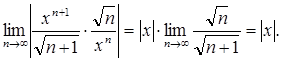
Если , т.е. , то в соответствии с признаком Даламбера абсолютной сходимости функционального ряда, исследуемый функциональный ряд сходится абсолютно на интервале .

Если , т.е. , то функциональный ряд расходится.

Исследуем заданный ряд в точках и .

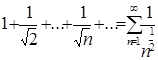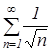При получим числовой положительный ряд . Это ряд Дирихле с . Известно, что если , то ряд расходится. Значит, функциональный ряд в точке расходится.

При получим числовой знакочередующийся ряд вида 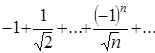. Он сходится, так как удовлетворяет условиям признака Лейбница сходимости знакочередующихся числовых рядов, т.е. и : .

Ряд, составленный из абсолютных величин элементов ряда 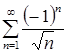, имеет вид и является расходящимся.

Значит, функциональный ряд сходится условно в точке x=1.

Итак, область сходимости исследуемого функционального ряда . Абсолютно ряд сходится на интервале .

Ответ: .

Преподаватель: Последний вид заданий, который мы с вами сегодня рассмотрим, - на нахождение суммы функционального ряда.

Пример №8 (№14 из [10], с комментариями преподавателя).

Найти сумму ряда:

.

Решение

По признаку Даламбера абсолютной сходимости функционального ряда можем записать:

.

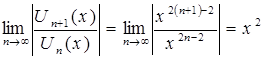Если , т.е. то функциональный ряд сходится абсолютно на интервале .

Если , т.е. , то исследуемый функциональный ряд расходится на указанных промежутках.

При функциональный ряд становится числовым положительным расходящимся рядом , так как не выполняется необходимое условие сходимости числового ряда, т.е. .