Исследование функциональных последовательностей и рядов в вузе
Домашнее задание: Практическое занятие №14 из [9].
Ниже приведены решенные номера домашнего задания:
Пример №36 (№95 из [10]).
Можно ли к ряду
![]()
применить теорему о дифференцировании функциональных рядов?
Решение
Функциональный ряд можно почленно продифференцировать, если члены ряда и производные его чл
енов непрерывны, а сам ряд и ряд, составленный из производных членов его ряда, сходятся равномерно на данном промежутке.
Рассмотрим заданный функциональный ряд 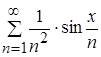 :
:
a) члены ряда являются непрерывными функциями для ![]() R,
R, ![]() N;
N;
б) так как 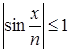 при
при ![]() R,
R, ![]() N, то справедливо неравенство
N, то справедливо неравенство 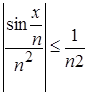 при
при ![]() R,
R, ![]() N;
N;
в) но 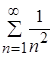 - числовой положительный сходящийся ряд (ряд Дирихле с
- числовой положительный сходящийся ряд (ряд Дирихле с ![]() );
);
г) значит, функциональный ряд 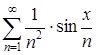 сходится равномерно и абсолютно при
сходится равномерно и абсолютно при ![]() R по признаку Вейерштрасса.
R по признаку Вейерштрасса.
Составим ряд из производных членов заданного функционального ряда
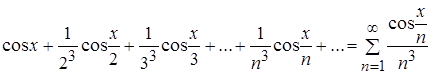 .
.
Исследуем полученный функциональный ряд:
a) члены ряда являются непрерывными функциями для ![]() R,
R, ![]() N;
N;
б) так как 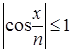 при
при ![]() R,
R, ![]() N, то справедливо неравенство
N, то справедливо неравенство 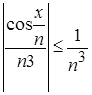 при
при ![]() R,
R, ![]() N;
N;
в) но 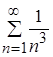 - числовой положительный сходящийся ряд (ряд Дирихле с
- числовой положительный сходящийся ряд (ряд Дирихле с ![]() );
);
г) значит, функциональный ряд 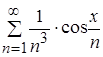 сходится равномерно и абсолютно при
сходится равномерно и абсолютно при ![]() R по признаку Вейерштрасса.
R по признаку Вейерштрасса.
Следовательно, заданный функциональный ряд 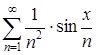 можно почленно дифференцировать.
можно почленно дифференцировать.
Ответ: Теорему о почленном дифференцировании применить можно.
Пример №36 (№96 из [10]).
Можно ли к ряду 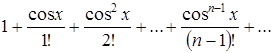 применить теорему об интегрировании функциональных рядов в любом конечном промежутке
применить теорему об интегрировании функциональных рядов в любом конечном промежутке ![]() ?
?
Решение
Функциональный ряд 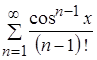 можно почленно интегрировать на отрезке
можно почленно интегрировать на отрезке ![]() , если на указанном промежутке его члены непрерывны, и ряд равномерно сходится.
, если на указанном промежутке его члены непрерывны, и ряд равномерно сходится.
Элементы функционального ряда 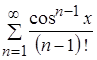 являются непрерывными функциями для
являются непрерывными функциями для ![]() R.
R.
Кроме того, по признаку Вейерштрасса заданный функциональный ряд равномерно и абсолютно сходится на R, а, значит, и на отрезке ![]() .
.
Действительно, так как:
а) ![]() для
для ![]() R,
R, ![]() N;
N;
б) 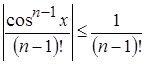 для
для ![]() R;
R;
в) 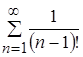 - числовой положительный сходящийся ряд. По признаку Даламбера
- числовой положительный сходящийся ряд. По признаку Даламбера 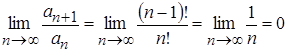 , 0<1.
, 0<1.
Значит, теорему о почленном интегрировании к функциональному ряду 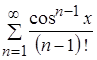 на отрезке
на отрезке ![]() применить можно.
применить можно.
Ответ: Можно почленно проинтегрировать функциональный ряд 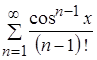 .
.
Пример №37 (№106 из [10]).
Дифференцируя прогрессию 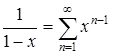 получить новые разложения. Решение
получить новые разложения. Решение
Ряд 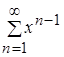 сходится на интервале
сходится на интервале ![]() , как сумма убывающей геометрической прогрессии. Производная общего члена заданного функционального ряда примет вид:
, как сумма убывающей геометрической прогрессии. Производная общего члена заданного функционального ряда примет вид: ![]() . Составим ряд из производных:
. Составим ряд из производных:
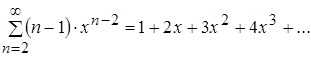 .
.
Исследуем полученный ряд на сходимость. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
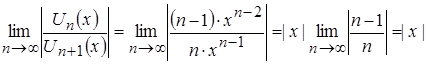 ,
,
если ![]() , т.е.
, т.е. ![]() , то ряд
, то ряд 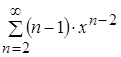 сходится абсолютно.
сходится абсолютно.
Ответ: При дифференцировании заданной прогрессии получен ряд 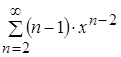 .
.
Пример №38 (№109 из [10]).
Убедиться, что ряд 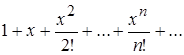 можно продифференцировать почленно.
можно продифференцировать почленно.
Решение
Исследуем заданный функциональный ряд на сходимость. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
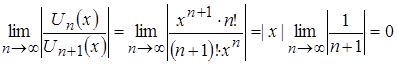 ,
,
Так как ![]() , то ряд
, то ряд ![]() сходится абсолютно при
сходится абсолютно при ![]() R. Тогда остаток ряда можно оценить с помощью неравенства
R. Тогда остаток ряда можно оценить с помощью неравенства ![]() , т.е.
, т.е.
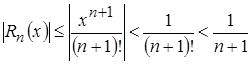 .
.
Другие рефераты на тему «Педагогика»:
- Инновационный подход к организации воспитательной работы в специальной школе-интернате
- Развитие вокально-национальной культуры в системе дополнительного образования
- Возможности использования музыки в эмоциональном развитии дошкольников с интеллектуальной недостаточностью
- Педагогическая психология
- Педагогические технологии
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
