Исследование функциональных последовательностей и рядов в вузе
Ответ: Доказана равномерная и абсолютная сходимость при ![]() .
.
Пример №18 (№89 из [10], c комментариями преподавателя).
С помощью признака Вейерштрасса показать, что ряд
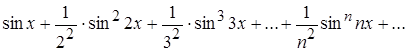
сходится равномерно в промежутке ![]() .
.
Решение
Так как 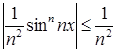 при
при ![]() R и числовой положительный ряд
R и числовой положительный ряд ![]() сходится, как обобщенный гармонический ряд с
сходится, как обобщенный гармонический ряд с ![]() , то заданный функциональный ряд сходится равномерно и абсолютно при любых значениях
, то заданный функциональный ряд сходится равномерно и абсолютно при любых значениях ![]() .
.
Ответ: Доказана равномерная и абсолютная сходимость для ![]() R.
R.
Пример №19 (№79 из [10], студент с помощью преподавателя).
Показать, что ряд 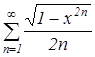 сходится равномерно на отрезке
сходится равномерно на отрезке ![]() .
.
Решение
Если ![]() , то
, то ![]() . Значит, числовой положительный ряд
. Значит, числовой положительный ряд 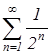 является мажорантным. По признаку Даламбера абсолютной сходимости числовых рядов имеем:
является мажорантным. По признаку Даламбера абсолютной сходимости числовых рядов имеем: 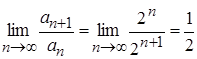 , так как
, так как ![]() , то числовой ряд сходится абсолютно.
, то числовой ряд сходится абсолютно.
Следовательно, по теореме Вейерштрасса равномерной и абсолютной сходимости функциональных рядов, ряд 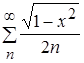 сходится при
сходится при ![]() равномерно и абсолютно.
равномерно и абсолютно.
Если ![]() , то ряд примет вид
, то ряд примет вид![]() - сходится. Значит, и заданный функциональный ряд сходится равномерно.
- сходится. Значит, и заданный функциональный ряд сходится равномерно.
Если ![]() , то ряд примет вид
, то ряд примет вид![]() - сходится. Значит, и заданный функциональный ряд сходится равномерно.
- сходится. Значит, и заданный функциональный ряд сходится равномерно.
Итак, ряд 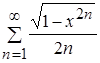 сходится равномерно и абсолютно на отрезке
сходится равномерно и абсолютно на отрезке ![]() .
.
Ответ: Доказана равномерная и абсолютная сходимость на отрезке ![]() . Пример №20 (№52 из [10], студент самостоятельно у доски).
. Пример №20 (№52 из [10], студент самостоятельно у доски).
Исследовать на равномерную сходимость ряд ![]() на всей числовой оси.
на всей числовой оси.
Решение
Так как ![]() при
при ![]() N и
N и ![]() R, то в качестве мажорантного ряда выберем
R, то в качестве мажорантного ряда выберем ![]() - числовой положительный ряд (ряд Дирихле). Он сходится. Следовательно, и ряд
- числовой положительный ряд (ряд Дирихле). Он сходится. Следовательно, и ряд 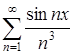 по теореме Вейерштрасса равномерно и абсолютно сходится, так как
по теореме Вейерштрасса равномерно и абсолютно сходится, так как 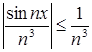 при
при ![]() R
R
Ответ: Доказана равномерная и абсолютная сходимость на интервале ![]() .
.
Пример №21 (№164 из [8], студент самостоятельно у доски).
Исследовать на равномерную сходимость ряд 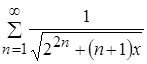 на интервале
на интервале ![]() .
.
Решение
Если ![]() , то
, то 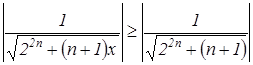 - условие равномерной сходимости не выполняется.
- условие равномерной сходимости не выполняется.
Если ![]() , то
, то 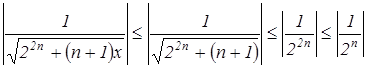 . Ряд
. Ряд ![]() мажорантный по отношению к ряду
мажорантный по отношению к ряду 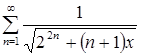 . По признаку Даламбера сходимости числовых рядов имеем:
. По признаку Даламбера сходимости числовых рядов имеем: 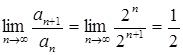 . Так как
. Так как ![]() , то числовой ряд сходится. Значит, по теореме Вейерштрасса равномерно сходимости функциональных рядов, так как
, то числовой ряд сходится. Значит, по теореме Вейерштрасса равномерно сходимости функциональных рядов, так как 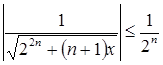 при
при ![]() , ряд
, ряд 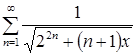 сходится равномерно и абсолютно.
сходится равномерно и абсолютно.
Ответ: Равномерно и абсолютно сходится при ![]() .
.
Преподаватель: Доказательство равномерной сходимости может быть и вспомогательной задачей, которую необходимо решить, чтобы выполнить основное задание.
Пример №22 (№94 из [10], с комментариями преподавателя).
Показать, что на луче ![]() функциональный ряд
функциональный ряд
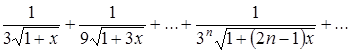
равномерно сходится. Начиная с какого номера ![]() , остаток ряда
, остаток ряда ![]() (независимо от значения
(независимо от значения ![]() ) удовлетворяет неравенству
) удовлетворяет неравенству ![]() ?.
?.
Решение
Воспользуемся признаком Вейерштрасса.
Так как при ![]() справедливо неравенство:
справедливо неравенство: ![]() , то элементы заданного функционального ряда на указанном промежутке не больше соответствующих членов положительного числового ряда
, то элементы заданного функционального ряда на указанном промежутке не больше соответствующих членов положительного числового ряда ![]() , т.е.
, т.е. 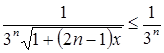 при
при ![]() .
.
Числовой положительный ряд ![]() сходится, так как представляет собой сумму убывающей геометрической прогрессии с
сходится, так как представляет собой сумму убывающей геометрической прогрессии с
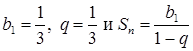 ,
, 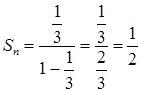 ,
, ![]() .
.
Другие рефераты на тему «Педагогика»:
- Формирование ролевой игры у умственно отсталых детей дошкольного возраста
- Обучение монологической речи учеников 10 класса на уроках английского языка
- Развитие коммуникативных навыков у младших школьников на уроках английского языка
- Коррекция профессиональных деструкций у педагогов
- Роль уроков музыки в формировании экологической культуры школьников
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
