Исследование функциональных последовательностей и рядов в вузе
Так как неравенства ![]() и
и ![]() равносильны, то, взяв
равносильны, то, взяв ![]() , где
, где ![]() - какое-нибудь целое положительное число, удовлетворяющее условию
- какое-нибудь целое положительное число, удовлетворяющее условию 48 src="images/referats/27276/image863.png">, приходим к неравенству
![]() . Итак, заданный функциональный ряд сходится абсолютно и равномерно при
. Итак, заданный функциональный ряд сходится абсолютно и равномерно при ![]() R. Члены ряда являются непрерывными функциями при
R. Члены ряда являются непрерывными функциями при ![]() R.
R.
Производная общего члена заданного функционального ряда примет вид:
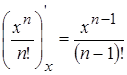 .
.
Исследуем ряд 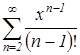 на сходимость. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
на сходимость. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
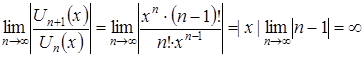 ,
,
так как ![]() , то условие абсолютной сходимости ряда не выполняется при
, то условие абсолютной сходимости ряда не выполняется при ![]() R. Следовательно, ряд
R. Следовательно, ряд 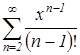 расходится.
расходится.
Значит, к заданному функциональному ряду нельзя применить теорему о почленном дифференцировании.
Ответ: Теорему о почленном дифференцировании к ряду ![]() применить нельзя.
применить нельзя.
Пример №39 (№115 из [10]).
Показать, что ряд 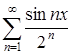 допускает почленное интегрирование на отрезке
допускает почленное интегрирование на отрезке ![]() , написать полученный при этом ряд.
, написать полученный при этом ряд.
Решение
Функциональный ряд 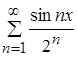 можно интегрировать почленно на отрезке
можно интегрировать почленно на отрезке ![]() , если на этом отрезке его члены непрерывны, и ряд равномерно сходится.
, если на этом отрезке его члены непрерывны, и ряд равномерно сходится.
Элементы функционального ряда 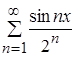 являются непрерывными функциями для
являются непрерывными функциями для ![]() R, значит, и на отрезке
R, значит, и на отрезке ![]() .
.
Кроме того, по признаку Вейерштрасса заданный функциональный ряд равномерно и абсолютно сходится на R, а, значит, и на отрезке ![]() . Действительно, так как:
. Действительно, так как:
а) ![]() для
для ![]() R,
R, ![]() N;
N;
б) 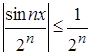 при
при ![]() R;
R;
в) 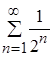 - числовой положительный сходящийся ряд (сумма убывающей геометрической прогрессии с
- числовой положительный сходящийся ряд (сумма убывающей геометрической прогрессии с 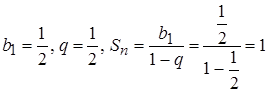 ).
).
Значит, теорему о почленном интегрировании можно применить к функциональному ряду 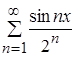 на отрезке
на отрезке ![]() .
.
Ряд полученный при почленном интегрировании заданного ряда, примет вид 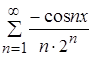 на отрезке
на отрезке ![]() .
.
Ответ: 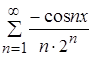 при
при ![]() .
.
Пример №40 (№119 из [10])
Определить область существования функции 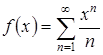 и исследовать ее на дифференцируемость во внутренних точках существования.
и исследовать ее на дифференцируемость во внутренних точках существования.
Решение
Определим область сходимости ряда 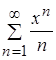 . По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
. По признаку Даламбера абсолютной сходимости функциональных рядов имеем:
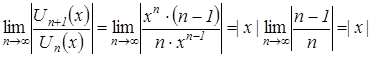 ,
,
если ![]() , т.е.
, т.е. ![]() , то заданный функциональный ряд сходится абсолютно.
, то заданный функциональный ряд сходится абсолютно.
При ![]() ряд примет вид
ряд примет вид 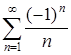 . Полученный ряд сходится условно, так как удовлетворяет условиям признака Лейбница (признак сходимости числовых знакочередующихся рядов), т.е.
. Полученный ряд сходится условно, так как удовлетворяет условиям признака Лейбница (признак сходимости числовых знакочередующихся рядов), т.е. ![]() и
и ![]() .
.
При ![]() ряд примет вид
ряд примет вид ![]() -расходящийся гармонический ряд.
-расходящийся гармонический ряд.
Значит, ![]() - область сходимости заданного ряда, причем элементы ряда являются непрерывными функциями на всей области сходимости.
- область сходимости заданного ряда, причем элементы ряда являются непрерывными функциями на всей области сходимости.
Найдем производную общего члена ряда: 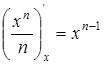 . Ряд из производных
. Ряд из производных 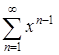 сходится при
сходится при ![]() , как сумма убывающей геометрической прогрессии. Причем, элементы ряда также являются непрерывными при
, как сумма убывающей геометрической прогрессии. Причем, элементы ряда также являются непрерывными при ![]() .
.
Значит, ряд 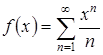 можно продифференцировать во всех внутренних точках интервала
можно продифференцировать во всех внутренних точках интервала ![]() .
.
Ответ: Заданный функциональный ряд можно почленно дифференцировать на интервале ![]() .
.
§9. Результаты пробация
В осеннем семестре 2003-2004 учебного года были апробированы лекционные и практические занятия, а также тест по теме "Функциональные последовательности и ряды" на втором курсе факультета математики и информатики СГПИ.
Материалы фондовых лекций по вышеуказанной теме были продемонстрированы студентам в электронном виде. Для проведения лекций использовался компьютер с TV-кодером и телевизор с большой диагональю экрана (71см). Текст лекции с жесткомагнитного диска подавался на экран и озвучивался лектором. Применяемая методика проведения лекционных занятий с использованием новейших информационных технологий позволила увеличить скорость подачи информации в 1,5 раза и улучшила качество содержания конспектов студентов.
Другие рефераты на тему «Педагогика»:
- Развитие познавательных интересов у дошкольников в процессе ознакомления с природой
- Методы обучения русскому языку
- Значение занятий по плаванию для укрепления организма ребенка дошкольного возраста
- Методы физического воспитания
- Формирование устойчивой мотивации к изучению иностранного языка на среднем этапе с использованием современных аудиовизуальных средств
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
