Исследование функциональных последовательностей и рядов в вузе

Замечание. Условие равномерной сходимости ряда на является лишь достаточным, но не необходимым, поэтому некоторые функциональные ряды, которые равномерно не сходятся, могут быть почленно проинтегрированы [20].

§10. Почленное дифференцирование функциональных рядов

Теорема 7. Пусть последовательность функций ight=25 src="images/referats/27276/image264.png">, непрерывно дифференцируемых на , и последовательность их производных равномерно сходятся на , тогда предел последовательности непрерывно дифференцируемых функций , т.е. , непрерывно дифференцируем на указанном отрезке и верно равенство:

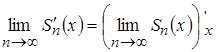или

.

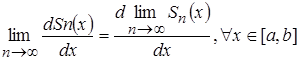Доказательство

Обозначим через предельную функцию последовательностей функций : .

По условию теоремы равномерно сходится к предельной функции на .

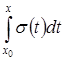На основании ранее доказанных теорем функция непрерывна на , следовательно, она будет интегрируема на, т.е. существует , он будет равен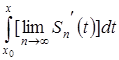 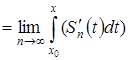(на основании теоремы о почленном интегрировании функциональных последовательностей).

По свойству определенного интеграла: 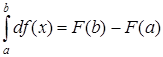, правую часть записанного выражения можно записать в виде следующего равенства: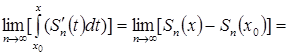 (на основании теоремы о предельной сумме сходящихся последовательностей) и видно, что функция дифференцируема для .

Известна теорема, что если функция дифференцируема в точке, то она непрерывна в этой точке. Значит, функция непрерывна .

В соответствии с теоремой, если функция непрерывна на , то она на нем интегрируема, т.е. существует 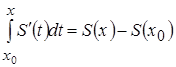. Следовательно, функция непрерывна в каждой точке .

Из пунктов 4),

5), и 6) следует, что функция непрерывно дифференцируема на указанном отрезке.

Теорема доказана [14].

Следствие. Пусть функции непрерывно дифференцируемы на и функциональные ряды: 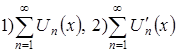равномерно сходятся на . Тогда сумма функционального ряда 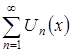непрерывно дифференцируема на указанном отрезке и верно равенство:

=

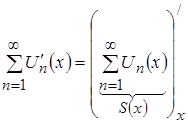(т.е. допустимо почленное дифференцирование у такого функционального ряда).

Доказательство

Обозначим предел частичных сумм , т.е. для функционального ряда 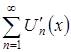. По условию следствия должны равномерно сходиться последовательности функций . На основании только что доказанной теоремы и функция непрерывно дифференцируема, т.е. . Последнее равенство можно переписать по-другому:

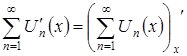.Теорема доказана [14].

Психолого-педагогические аспекты и методические рекомендации изучения темы математического анализа. "Функциональные последовательности и ряды"

Психолого-педагогические аспекты образования в высшей школе

В настоящее время нет, пожалуй, более спорной проблемы в педагогике и психологии высшей школы, чем проблема воспитания студентов. Вуз служит не только и может быть не столько для передачи специальных знаний, сколько для развития и воспроизведения особого культурного слоя, важнейшим элементом которого является и сам специалист. Специалиста как представителя определенной культуры характеризует не только специфический набор знаний и умений, но и определенное мировоззрение, жизненные установки и ценности, особенности профессионального поведения и т.п. Поэтому он не только передает студенту знания и профессиональные умения, а приобщает его к определенной культуре, и чтобы эта культура развивалась и воспроизводилась, необходимы живые люди, живое человеческое общение [19].

Воспитывать - это в значительной степени означает строить систему взаимоотношений между людьми. В современной педагогике (а также в психологии) начинает преобладать подход к воспитанию не как к целенаправленному формированию личности, в соответствии с выбранным идеалом, а как к созданию условий для саморазвития личности. Ведь уникальность и неповторимость каждой личности составляют богатство всего общества, и всякое искусственное ограничение свободного проявления и развития личности подрывает ее творческие потенции.

В своем развитии личность стремится выйти за пределы самое себя, стремится к росту, направление которого воспитатель не может предугадать заранее и он не имеет права принимать сколько-нибудь ответственные решения за воспитуемого, какими бы само собой разумеющимися эти решения не казались ему. Самый главный прием воспитания - это принятие человека таким, какой он есть, без прямых оценок и наставлений. Только в этом случае будет сохраняться у воспитателя контакт с воспитуемым, что является естественным условием плодотворного взаимодействия обоих участников воспитательного процесса.