Исследование функциональных последовательностей и рядов в вузе

Вопрос 1: Какая последовательность называется равномерно сходящейся?

Ответ: Определение №1. Функциональная последовательность называется равномерно сходящейся на множестве , если существует функция

, в которой она равномерно сходится на множестве . Обозначение:

[14].

Вопрос 2: Какой функциональный ряд называется равномерно сходящимся? Сформулировать определение такого ряда, используя понятие последовательности его частичных сумм.

Ответ: Определение №2. Если последовательность частичных сумм функционального ряда равномерно сходится к функции на множестве , то ряд равномерно сходится на множестве [21].

Вопрос 3: Дать определение равномерно сходящегося функционального ряда, используя понятие остатка функционального ряда.

Ответ: Определение №3. Представим сумму функционального ряда в виде: , где [-остаток функционального ряда].

Определение №4. Сходящийся функциональный ряд 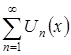называется равномерно сходящимся в некоторой области , если для каждого сколь угодно малого числа найдется такое положительное число , что при выполняется неравенство для любого из области . При этом сумма равномерно сходящегося ряда 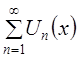в области , где (n=1,2,3…) - непрерывные функции в области , есть непрерывная функция.

Вопрос 4: Сформулировать достаточный признак равномерной сходимости функционального ряда - признак Вейерштрасса.

Ответ: Теорема. Пусть даны два ряда: функциональный , элементами которого являются функции , определенные на множестве, и числовой положительный сходящийся ряд . Тогда, если для всех выполняется неравенство , то функциональный ряд равномерно и абсолютно сходится на множестве .

Преподаватель: А теперь рассмотрим задание на исследование равномерной сходимости функционального ряда.

Пример №16 (№349 из [7], c комментариями преподавателя).

Показать, что ряд

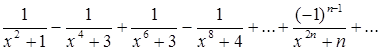
сходится равномерно при всех действительных значениях .

Решение

Данный ряд при любом значении сходится по признаку Лейбница, поэтому его остаток оценивается с помощью неравенства , т.е.

.

Так как неравенства и равносильны, то, взяв , где - какое-нибудь целое положительное число, которое удовлетворяет условию , приходим к неравенству . Итак, данный ряд сходится рав-номерно в промежутке при всех .

Ответ: Доказана равномерная сходимость для R.

Пример №17 (№51 из [10], студент у доски с помощью преподавателя).

Исследовать на равномерную сходимость ряд

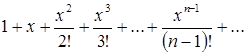
на любом конечном интервале.

Решение

Докажем, что каково бы ни было число , данный ряд сходится равномерно и абсолютно в круге радиусом , т.е. .

Заданный ряд сходится при любом значении , в частности, при , получаем числовой ряд: .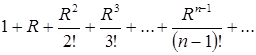

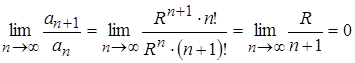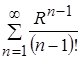Исследуем его на абсолютную сходимость, применив признак Даламбера . Так как , то ряд сходится, причем абсолютно.

Возьмем этот ряд в качестве мажорантного, по признаку Вейерштрасса равномерной сходимости функционального ряда 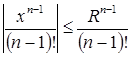при .

Значит, заданный ряд 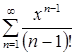равномерно и абсолютно сходится при .