Исследование функциональных последовательностей и рядов в вузе
Так как по условию достаточности выполняется неравенство 3) Значит, А это означает, что функциональная последовательность будет сходиться на множестве Х, так как будет выполняться неравенство: Теорема доказана [14].
§6. Критерий Коши равномерной сходимости функционального ряда
Теорема 2. Для того чтобы функциональный ряд Доказательство
1) Составим разность частичных сумм функционального ряда 2) Если будут выполняться неравенства: Теорема доказана [14].
§7. Достаточный признак равномерной и абсолютной сходимости функционального ряда (признак Вейерштрасса)
Теорема 3. Пусть даны два ряда: функциональный Доказательство:
Пусть выполняются все условия теоремы.
Так как по условию теоремы числовой ряд Так как это положительный числовой ряд, то неравенство примет вид:
По условию теоремы Если Докажем равномерность сходимости функционального ряда. Из неравенства По свойству транзитивности: Теорема доказана [21].
Замечание. Положительный сходящийся числовой ряд, связанный с функциональным рядом, называется мажорантным или мажорирующим [14].
Пример №3: Доказать, что функциональный ряд Решение
1) Так как 2) Cравним общие элементы функционального и числового рядов: ![]() , то какое бы х из Х не было взято, функциональная последовательность
, то какое бы х из Х не было взято, функциональная последовательность ![]() будет числовой последовательностью, а для числовой последовательности выполняется критерий Коши сходимости числовой последовательности
будет числовой последовательностью, а для числовой последовательности выполняется критерий Коши сходимости числовой последовательности ![]() сходится.
сходится.
![]() у функциональной последовательности
у функциональной последовательности ![]() существует конечный предел, а это доказывает существование предельной функции для функциональной последовательности:
существует конечный предел, а это доказывает существование предельной функции для функциональной последовательности: ![]() . Кроме того,
. Кроме того, ![]() .
.
![]() , перейдем к пределу при
, перейдем к пределу при ![]() , а n-const, получим:
, а n-const, получим: ![]() - условие равномерной сходимости функциональной последовательности по определению.
- условие равномерной сходимости функциональной последовательности по определению.
![]() равномерно сходился на множестве X, необходимо и достаточно, чтобы
равномерно сходился на множестве X, необходимо и достаточно, чтобы ![]() 0,
0, ![]() N,
N, ![]() ,
, ![]() ,
, ![]() N и
N и ![]() выполнялось неравенство:
выполнялось неравенство:
![]()
![]()
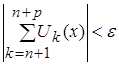 .
.
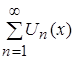 :
:
![]() .
.
![]() , то это означает, что последовательность частичных сумм функционального ряда
, то это означает, что последовательность частичных сумм функционального ряда 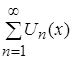 равномерно сходится на множестве Х. А по определению равномерной сходимости функционального ряда, исследуемый функциональный ряд будет сходиться на множестве Х.
равномерно сходится на множестве Х. А по определению равномерной сходимости функционального ряда, исследуемый функциональный ряд будет сходиться на множестве Х.
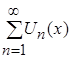 , элементами которого являются функции
, элементами которого являются функции ![]() , определенные на множестве Х, и числовой положительный сходящийся ряд
, определенные на множестве Х, и числовой положительный сходящийся ряд 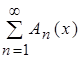 . Тогда, если для всех
. Тогда, если для всех ![]() выполняется неравенство
выполняется неравенство ![]() , то функциональный ряд
, то функциональный ряд 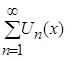 равномерно и абсолютно сходится на множестве Х.
равномерно и абсолютно сходится на множестве Х.
![]() сходится, то в соответствии со свойством числового ряда, его остаток должен стремится к нулю, т.е.
сходится, то в соответствии со свойством числового ряда, его остаток должен стремится к нулю, т.е. ![]() или
или ![]() .
.
![]()
![]() выполняется неравенство:
выполняется неравенство: ![]() . Поэтому, при
. Поэтому, при ![]() выполняется и такое неравенство:
выполняется и такое неравенство: 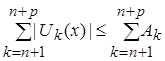 .
.
![]() , то неравенство примет вид:
, то неравенство примет вид: 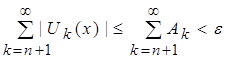 (с учетом пункта 2). По свойству транзитивности
(с учетом пункта 2). По свойству транзитивности 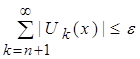 - это остаток положительного функционального ряда, стремящегося к нулю при
- это остаток положительного функционального ряда, стремящегося к нулю при ![]() . Значит, функциональный ряд
. Значит, функциональный ряд 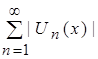 будет сходиться по свойству рядов. Известно, что если ряд абсолютно сходится, то он просто сходится. Значит, функциональный ряд
будет сходиться по свойству рядов. Известно, что если ряд абсолютно сходится, то он просто сходится. Значит, функциональный ряд 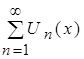 сходится.
сходится.
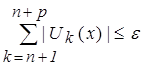 и, используя свойства модуля суммы двух действительных чисел (
и, используя свойства модуля суммы двух действительных чисел (![]() ) можно переписать это неравенство так:
) можно переписать это неравенство так:
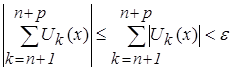 .
.
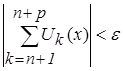 - условие равномерности сходимости функционального ряда на множестве Х.
- условие равномерности сходимости функционального ряда на множестве Х.
![]() абсолютно и равномерно сходится на всей числовой прямой.
абсолютно и равномерно сходится на всей числовой прямой.
![]() ,
, ![]() N,
N, ![]() R, то в качестве мажорантного ряда выберем
R, то в качестве мажорантного ряда выберем ![]() при
при ![]() R.
R.
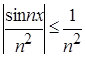 , при
, при ![]() R. Следовательно,
R. Следовательно, 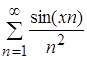 сходится абсолютно и равномерно на R, так как
сходится абсолютно и равномерно на R, так как 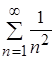 - положительный сходящийся ряд (ряд Дирихле с
- положительный сходящийся ряд (ряд Дирихле с ![]() ) [4]. Замечание. Признак Вейерштрасса является лишь достаточным условием равномерной сходимости функционального ряда [14].
) [4]. Замечание. Признак Вейерштрасса является лишь достаточным условием равномерной сходимости функционального ряда [14].
Другие рефераты на тему «Педагогика»:
Поиск рефератов
Последние рефераты раздела
