Исследование функциональных последовательностей и рядов в вузе
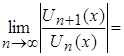
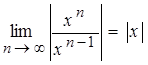 ,
,
Если ![]() , т.е.
, т.е. ![]() , то заданный функциональный ряд
, то заданный функциональный ряд 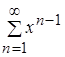 сходится абсолютно
сходится абсолютно
на интервале ![]() .
.
Если ![]() , т.е.
, т.е. ![]() , то ряд
, то ряд ![]() расходится в соответствии с признаком Даламбера абсолютной сходимости функционального ряда.
расходится в соответствии с признаком Даламбера абсолютной сходимости функционального ряда.
При![]() функциональный ряд становится числовым знакочередующимся рядом вида 1-1+1-…. Он расходится, так как не удовлетворяет ни одному условию признака Лейбница: а)
функциональный ряд становится числовым знакочередующимся рядом вида 1-1+1-…. Он расходится, так как не удовлетворяет ни одному условию признака Лейбница: а) ![]() ; б)
; б) ![]() . Значит, функциональный ряд
. Значит, функциональный ряд 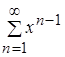 в точке
в точке ![]() расходится.
расходится.
При ![]() функциональный ряд становится числовым положительным рядом вида 1+1+1+…. Он расходится, так как не выполняется необходимое условие сходимости числового ряда, т.е.
функциональный ряд становится числовым положительным рядом вида 1+1+1+…. Он расходится, так как не выполняется необходимое условие сходимости числового ряда, т.е. ![]() . Значит, функциональный ряд
. Значит, функциональный ряд ![]() в точке
в точке ![]() расходится.
расходится.
Таким образом, областью абсолютной сходимости исследуемого функционального ряда является интервал ![]() .
.
Ответ: ![]() .
.
Пример №12 (№38 из [10]).
Найти область сходимости ряда
![]()
Решение. По признаку Даламбера абсолютной сходимости функционального ря-да имеем:
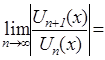
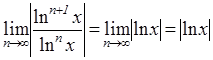 .
.
Если![]() , т.е.
, т.е. ![]() ,
, ![]() или
или ![]() , то функциональный ряд сходится абсолютно на интервале
, то функциональный ряд сходится абсолютно на интервале 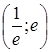 .
.
Если ![]() , т.е.
, т.е. 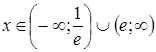 , то ряд
, то ряд ![]() расходится.
расходится.
При ![]() функциональный ряд становится числовым знакочередующимся рядом
функциональный ряд становится числовым знакочередующимся рядом ![]() . Он расходится, так как не удовлетворяет ни одному условию признака Лейбница: а)
. Он расходится, так как не удовлетворяет ни одному условию признака Лейбница: а) ![]() ; б)
; б) ![]() .
.
Значит, функциональный ряд ![]() расходится в точке
расходится в точке ![]() .
.
При ![]() функциональный ряд
функциональный ряд ![]() становится положительным числовым рядом
становится положительным числовым рядом ![]() . Он является расходящимся, так как не выполняется необходимое условие сходимости числового ряда
. Он является расходящимся, так как не выполняется необходимое условие сходимости числового ряда ![]() .
.
Значит, функциональный ряд ![]() расходится в точке
расходится в точке ![]() .
.
Таким образом, область абсолютной сходимости исследуемого ряда есть интервал 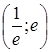 .
.
Ответ: 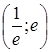 .
.
Пример №13 (№5 из [10]).
Найти область сходимости функционального ряда:
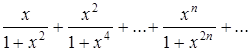
Решение
По признаку Даламбера абсолютной сходимости функционального ря-да имеем:
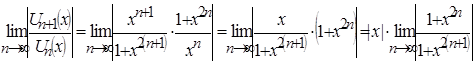 .
.
Если ![]() , то
, то
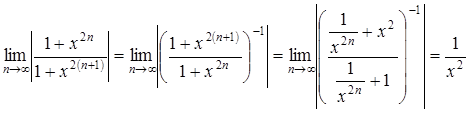 .
.
Тогда 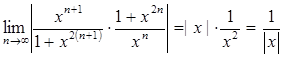 .
.
Если ![]() , т.е.
, т.е. ![]() , то заданный ряд сходится абсолютно.
, то заданный ряд сходится абсолютно.
Если ![]() , то
, то 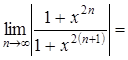 1.
1.
Тогда, 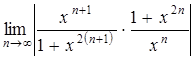 =
=![]() . Если
. Если ![]() , т.е.
, т.е. ![]() , то заданный функциональный ряд сходится абсолютно.
, то заданный функциональный ряд сходится абсолютно.
Отсюда, ![]() - интервал сходимости заданного функционального ряда.
- интервал сходимости заданного функционального ряда.
Определим сходимость ряда в точках ![]() и
и ![]() .
.
Если ![]() , то ряд примет вид
, то ряд примет вид ![]() - числовой знакочередующийся ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е.
- числовой знакочередующийся ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. ![]() . Следовательно, заданный функциональный ряд расходится в точке
. Следовательно, заданный функциональный ряд расходится в точке ![]() .
.
Если ![]() , то ряд примет вид
, то ряд примет вид ![]() - числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е.
- числовой положительный ряд. Он расходится, так как необходимое условие сходимости числового ряда не выполняется, т.е. ![]() . Следовательно, исследуемый функциональный ряд расходится в точке
. Следовательно, исследуемый функциональный ряд расходится в точке ![]() .
.
Значит, ![]() - область абсолютной сходимости заданного функционального ряда. Ответ:
- область абсолютной сходимости заданного функционального ряда. Ответ: ![]() .
.
Другие рефераты на тему «Педагогика»:
Поиск рефератов
Последние рефераты раздела
- Тенденции развития системы высшего образования в Украине и за рубежом: основные направления
- Влияние здоровьесберегающего подхода в организации воспитательной работы на формирование валеологической грамотности младших школьников
- Характеристика компетенций бакалавров – психологов образования
- Коррекционная программа по снижению тревожности у детей младшего школьного возраста методом глинотерапии
- Формирование лексики у дошкольников с общим недоразвитием речи
- Роль наглядности в преподавании изобразительного искусства
- Активные методы теоретического обучения
