Плоские кривые

На рисунке 2 все эти случаи предусмотрены, причём соответствующие элементы помечены одинаковыми цифрами.

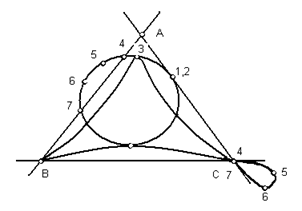Рис. 2

Из сказанного следует, что если преобразуемая кривая второго порядка пересекает стороны координатного треугольника в шести точках, то кривая четвёртого порядка будет иметь три узловые точки; если эти шесть точе

к мнимые, то им будут соответствовать три изолированные точки; если они попарно совпадают, то соответствующая кривая 4-го порядка будет иметь три точки возврата.

Особенности формы этой кривой зависят также от того, пересекает ли кривая второго порядка стороны координатного треугольника или их продолжения. Частные формы кривых, зависящие от этого обстоятельства, представлены на рисунке 3 – 6, где в качестве преобразуемой кривой второго порядка взята окружность.

Проследить особенности формы получающихся при квадратичном преобразовании кривых 4-го порядка можно, осуществляя преобразование заданной кривой второго порядка аналитически, но можно воспользоваться и графическим способом осуществления такого преобразования.

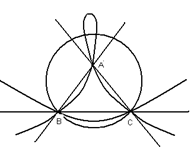Рис. 3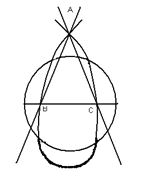Рис. 4

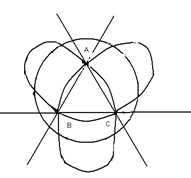Рис. 5Рис. 6

Если прямая с1 проходит через вершину координатного треугольника, то при преобразовании ей будут соответствовать две прямые – прямая с2, проходящая через ту же вершину, и противолежащая сторона треугольника (кривая второго порядка, которая должна соответствовать прямой в общем случае, эдесь распадается). Углы, составляемые прямой с1 и прямой с2 с биссектрисой угла А равны (рис. 7). Это обстоятельство и определяет графический способ осуществления квадратичного преобразования; а именно, чтобы найти точку Р2, соответствующую заданной точке Р1 с какой-либо вершиной треугольника, например с А, и проводим через вершину А прямую с2, симметричную прямой Р1А относительно биссектрисы угла А (рис. 8). Проводя аналогичное построение относительно вершины В, получим искомую точку Р2 как точку пересечения найденных прямых.

Осуществляя графическим путём квадратичное преобразование для ряда точек преобразуемой кривой, мы получим соответствующие точки новой кривой.

Графический способ даёт возможность определить наличие бесконечно удалённых точек кривой 4-го порядка, получаемой в результате квадратичного пребразования некоторой кривой второго порядка.

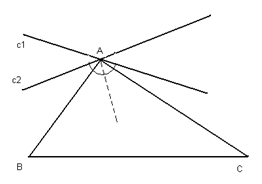Рис. 7

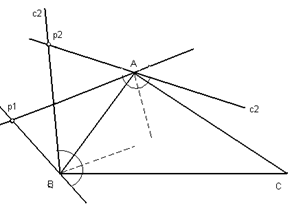Рис. 8

Для этого потребуется уравнение бесконечно удалённой прямой в трилинейных координатах [1].

Квадратичное преобразование устанавливает соответствие между точками описанной около координатного треугольника окружности и точками бесконечно удалённой прямой.

Отсюда следует, что кривая 4-го порядка, получаемая в результате квадратичного преобразования кривой 2-го порядка, будет иметь бесконечно удалённые точки лишь в том случае, если преобразуемая кривая пересекает окружность, описанную около координатного треугольника.

Чтобы определить направление в котором удалена точка кривой в бесконечность достаточно построить указанным выше графическим путём образ точки пересечения кривой с описанной около координатного треугольника окружностью.

2) Эллиптические кривые

Более сложными по своей природе являются кривые первого рода. Правые части их параметрических уравнений могут быть выражены эллиптическими функциями параметра, в силу чего такие кривые называют эллиптическими, и при изучении их широко пользуются свойствами эллиптических функций.

Подобно тому, как рациональные кривые 4-го порядка могут быть получены квадратичным преобразованием кривых второго порядка, эллиптические кривые 4-го порядка получаются квадратичным преобразованием кривых третьего порядка, не имеющих двойных точек и проходящих через две вершины координатного треугольника.

3) Циркулярные кривые

Циркулярные кривые являются алгебраическими кривыми, проходящими через циклические точки плоскости. Уравнение окружности, записанное в однородных координатах, имеет вид Точки пересечения этой окружности с несобственной прямой х3=0 определяются системой . Полагая х1=1, находим эти точки J1 (1, i, 0) и J2 (1, – i, 0). Так как изменение коэффициентов А, В, С в уравнении окружности не изменяет найденных координат, то можно утверждать, что всякая окружность проходит через точки J1 и J2, которые являются несобственными и мнимыми точками этой окружности и называются круговыми или циклическими точками плоскости.

4) Бициркулярные кривые

Эти кривые получаются в результате стереографической проекции линии пересечения поверхности шара с поверхностью второго порядка, не проходящей через центр проекции.

Интересными свойствами обладают бициркулярные кривые 4-го порядка, если они одновременно являются рациональными кривыми. Будучи рациональными, эти кривые должны иметь три двойные точки, но две двойные точки их должны совпадать с циклическими точками плоскости, и следовательно, они будут иметь только одну двойную точку, не являющуюся бесконечно удалённой.

Общее уравнение таких кривых может быть записано в виде

(x2 + y2) + (dx + ey) (x2 + y2) + ax2 + bxy + cy2 = 0. (1)

Уравнение касательной в двойной точке имеет вид

ax2 + bxy + cy2 =0.

В зависимости от знака (или равенства нулю) дискриминанта b2 – 4ac двойная точка кривой окажется изолированной, точкой возврата или узловой.

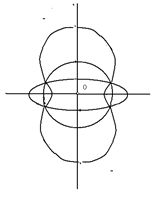Рис. 9Рис. 10

Бициркулярные рациональные кривые 4-го порядка могут быть образованы инверсией кривой второго порядка, но при условии, что полюс инверсии не лежит на этой кривой [1].

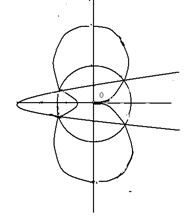Рис. 11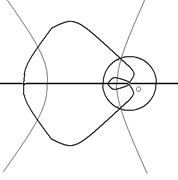Рис. 12

На рисунке 9 представлена инверсия эллипса, причём полюс инверсии находится в центре эллипса, который является изолированной точкой кривой. На рис. 10 и 11 приведена инверсия параболы, а на рис. 12 – инверсия гиперболы, причём полюс инверсии находится в фокусе гиперболы.

б) трансцендентные кривые

Трансцендентными называются кривые, уравнения которых, будучи записаны в прямоугольной системе координат, не являются алгебраическими.

Разлагая в ряд правую часть уравнения такой, например, трансцендентной кривой, как y = sin x, мы получим уравнение, содержащее алгебраические функции, однако число членов в нём будет неограниченным, а степень – бесконечно большой. Это даёт основание рассматривать трансцендентные кривые как алгебраические линии бесконечно высокого порядка. Соответственно этому можно полагать, что характерные точки алгебраических кривых (точки пересечения с прямой, точки перегиба, особые точки и т.д.) у трансцендентных кривых могут встречаться в бесконечном количестве. И это на самом деле так: трансцендентная кривая может пересекать прямую в бесконечном числе точек, у неё может быть бесконечное множество вершин даже на сколь угодно малом интервале (например, у кривой вблизи начала координат), бесконечное количество точек перегиба, асимптот и т.д.

 Скачать реферат