Теоретические основы математических и инструментальных методов экономики

Если x, y - два фиксированных элемента множества M, то есть действительное число, однако, полагая x и y равными всевозможным элементам множества M, получим, что является функцией двух переменных x, y. Эта функция называется метрикой данного пространст

ва.

Определение. Линейное пространство называется нормированным, если каждому элементу x этого пространства поставлено в соответствие действительное число (норма x ), причем выполнены следующие аксиомы:

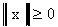1. для любого x, причем 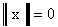тогда и только тогда, когда ;
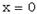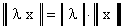2. для любого x и любого комплексного ;
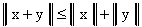3. для любых x, y из данного пространства.

Для линейных пространств над полем действительных чисел также вводится понятие нормированного пространства с теми же аксиомами.

Неравенство, фигурирующее в третьей аксиоме, называется неравенством Минковского.

Простейшими примерами нормированных пространств могут служить множества действительных чисел R и комплексных чисел C, где в качестве нормы числа рассматривается его модуль, а также пространство векторов на плоскости (или в пространстве) с нормой, равной длине вектора.

В пространстве непрерывных функций на (действительном или комплексном) норму можно ввести, например, следующими способами:

, .

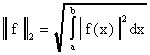Отметим теперь следующий важный факт. В любом линейном нормированном пространстве можно ввести метрику следующим образом:

При этом выполнение первой аксиомы метрического пространства следует из первой аксиомы нормированного пространства. Выполнение второй аксиомы также очевидно:

.

Наконец, выполнение третьей аксиомы метрического пространства следует из неравенства Минковского:

Итак, любое линейное нормированное пространство можно сделать метрическим пространством указанным выше естественным способом (так, указанные нами нормы в пространстве непрерывных функций порождают соответственно равномерную и среднеквадратичную метрику, т.е. порождают пространства и соответственно). Обратное утверждение, вообще говоря, неверно: не в любом метрическом пространстве можно ввести норму, поскольку понятие нормы вводится лишь в линейном пространстве, а метрическое пространство может не быть наделено линейной структурой. Однако, если метрическое пространство наделено линейной структурой (является линейным пространством), то его всегда можно сделать нормированным, введя норму

Пусть -- вещественное -мерное пространство, в котором задан базис . Тогда векторы и из задаются своими координатами:

Скалярное произведение векторов, обозначаеся оно обычно , задается формулой

В отличие от обычного трехмерного пространства, где с помощью транспортира и линейки можно измерить угол между векторами и длину вектора, в -мерном пространстве ни угол между векторами, ни длину вектора измерить невозможно (как можно, например, измерить длину многочлена или угол между многочленами?). Поэтому ортонормированным в -мерном пространстве называется тот базис, в котором скалярное произведение вычисляется по формуле (18.3).

Если 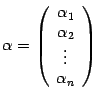, 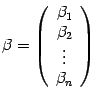-- координатные столбцы векторов и , то скалярное произведение можно задать формулой

Предоставляем читателю самостоятельно убедиться в совпадении этой формулы с формулой (18.3)

Определение 18.5 Вещественное линейное пространство, в котором задано скалярное произведение называется евклидовым пространством.

В трехмерном пространстве с помощью склярного произведения определялся угол между векторами. В евклидовом пространстве тоже можно определить угол между векторами. Но угол в -мерном пространстве не имеет существенного значения, кроме одного случая. В трехмерном проcтранстве два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.

 Скачать реферат