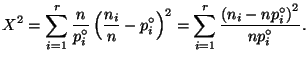Теоретические основы математических и инструментальных методов экономики

Можно показать, что стратегия, оптимальная по Нейману-Пирсону, по-прежнему сводится к сравнению величины отношения правдоподобия с некоторым пороговым значением , определяемым в данном случае требуемым значением вероятности ложной тревоги =0 width=23 height=23 src="images/referats/9797/image334.png">.

Значимости уровень статистического критерия, вероятность ошибочно отвергнуть основную проверяемую гипотезу, когда она верна. В теории статистической проверки гипотез З. у. называется вероятностью ошибки первого рода. Понятие "З. у." возникло в связи с задачей проверки согласованности теории с опытными данными. Если, например, в результате наблюдений регистрируются значения n случайных величин X1, ., Xn и если требуется по этим данным проверить гипотезу Н, согласно которой совместное распределение величин X1, ., Xn обладает некоторым определённым свойством, то соответствующий статистический критерий конструируется с помощью подходящим образом подобранной функции Y = f (X1, ., Xn); эта функция обычно принимает малые значения, когда гипотеза Н верна, и большие значения, когда Н ложна. В частности, если X1, ., Xn - результаты независимых измерений некоторой известной постоянной а и гипотеза Н представляет собой предположение об отсутствии в результатах измерений систематических ошибок, то для проверки Н разумно в качестве Y выбрать (2m - n)2, где m - количество тех результатов измерений X1, которые превышают истинное значение а. Наблюдаемое в опыте большое значение Y можно рассматривать как значимое статистическое опровержение гипотетического согласия между результатами наблюдений и проверяемой гипотезой. Соответствующий критерий значимости представляет собой правило, согласно которому значимыми считаются значения Y, превосходящие заданное критическое значение у. В свою очередь выбор величины у определяется заданным З. у., который в случае справедливости гипотезы Н совпадает с вероятностью события {Y>y}.

Мы рассматриваем независимую выборку , обозначая неизвестную функцию распределения . Нас интересует вопрос о том, согласуются ли данные наблюдений с простой гипотезой

где -- некоторая конкретная фиксированная функция распределения.

Вначале разобъем множество на конечное число непересекающихся подмножеств . Пусть -- вероятность, соответствующая функции распределения , обозначим Очевидно, что

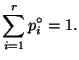
Теперь сделаем группировку данных аналогично процедуре, описанной в 6.3, а именно, определим

Очевидно, что в силу случайных колебаний эмпирические частоты будут отличаться от теоретических вероятностей . Чтобы контролировать это различие, следует подобрать хорошую меру расхождения между экспериментальными данными и гипотетическим теоретическим распределением. По аналогии с идеей метода наименьших квадратов в качестве такой меры расхождения можно взять, например, 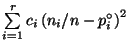, где положительные числа можно выбирать более или менее произвольно. Как показал К. Пирсон, если выбрать , то полученная величина будет обладать рядом замечательных свойств. Таким образом, положим

Подчеркнем, что величина вычисляется по выборке. Функцию принято называть статистикой Пирсона. Обсудим ее свойства.

Поведение , когда гипотеза верна.

Речь идет о поведении при увеличении объема выборки: .

Теорема К. Пирсона. Предположим, что гипотеза верна. Тогда при распределение величины сходится к распределению хи-квадрат с степенью свободы, то есть,

Практический смысл этой теоремы в том, что при большом объеме выборки распределение можно считать распределением хи-квадрат с степенью свободы.

Поведение , когда гипотеза неверна.

Предположим теперь, что и разбиение таково, что

где вероятности вычислены по функции распределения . Тогда можно показать (см., например, [13, § 10.4]), что

 Скачать реферат