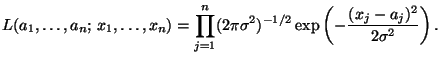Теоретические основы математических и инструментальных методов экономики

Начнем с очень простого примера. Предположим, что есть три образца некоторого материала, массы которых , и неизвестны. В наличии имеются весы, допускающие случайную нормально рас

пределенную погрешность. Образцы взвешивают раздельно, получая при этом показания весов , и соответственно. Затем три образца взвешивают вместе и получают показания весов . Если допустить, что весы всякий раз делают независимую ошибку, то, как правило, окажется, что .

Если бы мы допустили ``идеальную'' ситуацию, когда весы определяют массу абсолютно точно, то, очевидно, в четвертом взвешивании не было бы никакого смысла. Что касается реального опыта, когда к теоретическим массам добавляются случайные ошибки, то интуитивно кажется, что четвертое взвешивание может содержать в себе полезную информацию. Вопрос только в том, как ее правильно обработать.

Общая линейная модель

Теперь сформулируем и обсудим общую модель, а затем вернемся к примеру.

Предположим, что неизвестные величины последовательно измеряются некоторым измерительным прибором, прибавляющим случайную ошибку, распределенную по нормальному закону . Считая эти измерения независимыми между собой и обозначая результаты этих измерений через соответственно, запишем

где -- независимые случайные величины, распределенные по закону . Основное априорное допущение состоит в том, что вектор принадлежит некоторому линейному подпространству евклидова -мерного пространства . Заметим, что измерения , полученные в результате опыта вовсе не обязаны принадлежать . Цель -- получить оценку для вектора неизвестных параметров , используя данные измерений .

Так как независимы и имеет распределение , нетрудно выписать функцию правдоподобия (т.е. совместную плотность распределения , см. также 6.6):

В качестве искомой оценки будем искать точку , в которой функция правдоподобия принимает максимальное значение:

Выражение (38) переписывается в следующем виде:

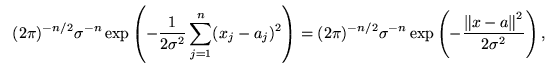
где 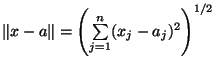-- обычное евклидово расстояние между векторами в . Отсюда видно, что максимальное значение достигается в такой точке , для которой

Из курса линейной алгебры известно, что такая точка единствена и представляет собой проекцию на подпространство : . Поскольку задача свелась к минимизации суммы квадратов, этот метод получил название метода наименьших квадратов.

Основы корреляционного анализа. Корреляционный момент и коэффициент корреляции. Функциональная и статистическая корреляция зависимости. Выборочный коэффициент корреляции. Корреляционное отношение как мера корреляционной связи.

Корреляционный анализ позволяет количественно оценить связи между большим числом взаимодействующих экономических явлений как между случайными величинами. Его применение делает возможным проверку различных экономических гипотез о наличии и силе связи между двумя величинами или группой величин. Корреляционный анализ тесно связан с регрессионным анализом, задача которого состоит в экспериментальном определении параметров корреляционных зависимостей (см. §2.5 ) между экономическими показателями путем наблюдения за характером их изменения. Одним из основных методов регрессионного анализа является метод наименьших квадратов, краткое содержание которого было изложено в §2.5. Модели, полученные с помощью регрессионного анализа, позволяют прогнозировать варианты развития экономических процессов и явлений, изучить тенденции изменения экономических показателей, т.е. служат инструментом научно-обоснованных предсказаний. Результаты прогноза являются исходным материалом для постановки реальных экономических целей и задач, для выявления и принятия наилучших управленческих решений, для разработки хозяйственной и финансовой стратегий в будущем.

 Скачать реферат