Биматричные игры. Поиск равновесных ситуаций

Рефераты / Экономико-математическое моделирование / Биматричные игры. Поиск равновесных ситуаций

1. Биматричные игры

Абсолютно любая управленческая деятельность не может существовать без конфликтных ситуаций. Это ситуации, где сталкиваются двое или больше сторон с разными интересами. Совершенно естественно, что каждая из сторон хочет решить конфликт в свою пользу и получить максимальную выгоду. Решение такой задачи может быть осложнено тем, что конфликтующая сторона не имеет полной и

нформации о конфликте в целом. Иначе можно сказать, что в конфликтной ситуации необходимо принять оптимальное решение в условиях неопределённости.

Для решения такого рода задач используется математическое моделирование. Введём несколько основных понятий. Математическая модель конфликтной игрой называется игрой. Стороны конфликта – игроки, действие игрока – ход, совокупность ходов – стратегия, результат игры – выигрыш.

Обязательным моментом перед решением задачи является выявление определённых правил. Как правило, эти правила представляют собой совокупность требований и ограничений на действия игроков, обмен информацией игроков о действиях противников, функций выигрышей противников и т.п. Правила должны быть чёткими, иначе игра не состоится.

К настоящему времени существует несколько способов классификации игр. Основным является деление на бескоалиционные конечные парные игры с выигрышами (матричные, позиционные, биматричные) и коалиционные. В данном реферате мы рассмотрим биматричные игры.

Игры с фиксированной суммы – игры, в которых интересы игроков хоть и не совпадают, но не являются полностью противоположными. Частным случаем являются биматричные игры.

Биматричная игра – это конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока (в каждой матрице строка соответствует стратегии игрока 1, столбец – стратегии игрока 2, на пересечении строки и столбца в первой матрице находится выигрыш игрока 1, во второй матрице – выигрыш игрока 2.)

Рассмотрим парную игру, в которой каждый из участников имеет следующие возможности для выбора своей линии поведения:

игрок А – может выбрать любую из стратегий А1, …, Аm;

игрок В – любую из стратегий В1, …, Вn;

Если игрок А выбрал стратегию Аi, игрок В – Вj, то в итоге выигрыш игрока А составит аij, игрока В – bij. Выигрыши игроков А и В можно записать в виде двух таблиц.

А=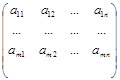

В=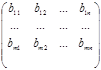

Таким образом, если интересы игроков различны, но не обязательно противоположны, для описания игры используются две платёжные матрицы. Данный факт и дал название подобным играм – биматричным.

2. Состояние равновесия в биматричных матрицах

Решением биматричной игры есть такое решение, которое в том или ином смысле устраивает обоих игроков. Данная формулировка очень расплывчата, что обуславливается тем, что в биматричных играх довольно трудно чётко сформулировать цели для игроков. Как один из возможных вариантов – желание игрока навредить своему сопернику в ущерб собственному выигрышу, или цель будет противоположна.

Обычно рассматриваются два подхода к решению биматричной игры. Первый – поиск равновесных ситуаций: ищутся условия, когда игра находится в некотором равновесии, которое невыгодно нарушать ни одному из игроков в отдельности. Второй – поиск ситуаций, оптимальных по Парето: нахождение условий, при которых игроки совместными усилиями не могут увеличить выигрыш одного игрока, не уменьшив при этом выигрыш другого.

Остановим своё внимание на первом подходе.

В данном подходе используются смешанные стратегии, т.е. случай, когда игроки чередуют свои чистые стратегии с определёнными вероятностями.

Пусть игрок А выбирает стратегию А1, с вероятностью р1, А2 – р2, …, Аm – pm, причём

Игрок В использует стратегию В1 с вероятностью q1, B2 – q2, …, Bn – qn, причём

В качестве критерия "удачности" игры возьмём математические ожидания выигрыша игроков, которые вычисляются по формулам:

Таким образом, можно сформулировать основное определение:

Распределение вероятностей Р* () и Q () определяют равновесную ситуацию, если для любых других распределений P и Q одновременно выполнены следующие неравенства:

Если равновесная ситуация существует, то отклонение от неё невыгодно самому игроку.

Также справедлива теорема Дж. Нэша. Всякая биматричная игра имеет хотя бы одну равновесную ситуацию в смешанных стратегиях.

3. Общий принцип решения биматричных игр

В первое неравенство системы последовательно подставляются все чистые стратегии игрока А, при предположении, что В придерживается своей оптимальной стратегии. Во второе неравенство подставляются все чистые стратегии игрока В, при предположении, что А придерживается своей оптимальной стратегии.

Полученная система m+n неравенств, решение которой дает значение элементов оптимальных смешанных стратегий (P*,Q*) и платежи, получаемые игроками в точке равновесия.

Пример: борьба за рынок.

А=