Модель парной регрессии

Содержание

ТЕМА 1. Выборка и генеральная совокупность

Задача 1

ТЕМА 2. Модель парной регрессии

Задача 12

ТЕМА 3. Модель множественной регрессии

Задача 13

ТЕМА 4. Нестационарные временные ряды

Задача 23

ТЕМА 1. Выборка и генеральная совокупность

Задача 1

1. Найдите среднее число государственных вузов в России, если данные их статистического учета с 1

994 по 2000г таковы

2. Найдите вариацию числа государственных вузов в России за 1994 2000гг

Решение

Определим выборочное среднее государственных вузов в России, по зависимости учитывая, что n=7.

Найдем вариацию числа государственных вузов в России за 1994-2000г по формуле:

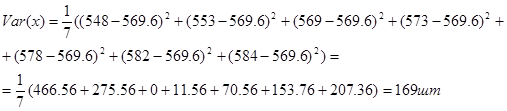
Таким образом, среднее число государственных вузов в России составляет 570 шт, а вариация 169.

ТЕМА 2. Модель парной регрессии

Задача 12

1. Предварительно вычисленная ковариация двух рядов составляет -4.32, а вариация ряда занятых в экономике равна 7,24. Средние выборочные равняются 68,5 и 5,87 соответственно. Оцените параметры линейного уравнения парной регрессии .

Решение

Оценим параметры линейного уравнения парной регрессии

Зная выборочные ковариацию и вариацию, вычислим параметр b по формуле (4)

а параметр a по зависимости

На основании полученных данных уравнение парной регрессии примет вид

Определим объясненную сумму квадратов отклонений ESS по формуле (8)

ТЕМА 3. Модель множественной регрессии

Задача 13

1. В таблице представлены ряды данных по продовольственным ресурсам (производству и импорту ) и личному потреблению картофеля y (млн. тонн) за 9 лет

Рассчитать вариации и попарные ковариации для этих рядов.

2. По данным таблицы построить уравнение регрессии, приняв личное потребление картофеля за зависимую переменную, а производство и импорт - за объясняющие. Рассчитать коэффициенты при объясняющих переменных.

3. Для регрессии, описывающей линейную зависимость потребления картофеля от производства и импорта , определить свободный коэффициент a.

4. Рассчитать значения личного потребления y картофеля, используя полученное в задаче уравнение регрессии.

5. Рассчитать общую, объясненную и необъясненную сумму квадратов отклонений для рассчитанной ранее регрессии для личного потребления y картофеля.

6. Используя полученные в предыдущем пункте TSS и ESS, рассчитать коэффициент детерминации для регрессии по картофелю.

Решение

Определим выборочные средние , и по формуле (1) при числе наблюдений: n=9

млн. т

млн. т

млн. т

Рассчитаем вариации и попарные ковариации для этих рядов. Вариации для рядов объясняющих переменных и можно вычислить по зависимостям (11)

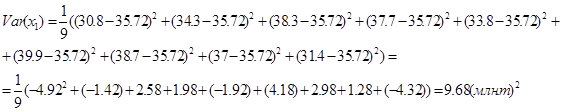
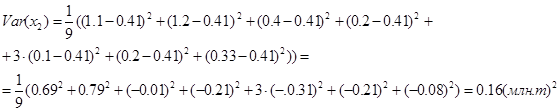
А вариацию зависимой переменной y по зависимости (12)

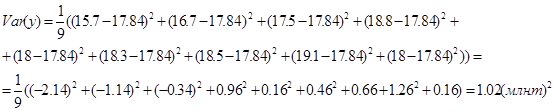
Попарные ковариации для этих рядов определяются по (13) как

 Скачать реферат