Геометрия Лобачевского

Рефераты / Математика / Геометрия Лобачевского

Эта модель определяется аналогично модели на плоскости. За пространство принимается открытое полупространство Р. «Плоскостями»» в нем служат содержащиеся в Р полусферы с центрами на граничной плоскости, а также перпендикулярные ей открытые полуплоскости. За «прямые»» принимаются полуокружности, перпендикулярные граничной плоскости (т. е. касательные к ним в концах перпендикуляры этой плоскости;

центры их лежат на граничной плоскости), а также перпендикулярные ей лучи. Роль «наложений»» играют композиции инверсий в сферах с центрами на граничной плоскости и отражений в перпендикулярных ей плоскостях.

Модель геометрии Лобачевского на поверхности

Оказывается, что геометрия Лобачевского реализуется на поверхностях постоянной отрицательной кривизной: внутренняя геометрия такой поверхности и есть геометрия Лобачевского. Только не на всей плоскости, а на той ее части, которая может быть представлена данной поверхностью. Вместе с тем доказано, что не существует (в трехмерном евклидовом пространстве) никакой поверхности, которая своей внутренней геометрией представляла бы всю плоскость Лобачевского.

Во внутренней геометрии поверхности роль прямолинейных отрезков играют кратчайшие линии (отрезки геодезических); роль наложений — такие отображения фигур, содержащихся в поверхности, которые сохраняют расстояния, измеряемые по этим кратчайшим линиям.

Самая известная из поверхностей постоянной отрицательной кривизны — псевдосфера — изображена на рис. 4-5.

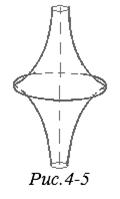
Реализацию геометрии Лобачевского на поверхностях постоянной отрицательной кривизны установил итальянский математик Бельтрами (в 1861 г.).

Впрочем, еще за 30 лет до него это установил, собственно, Миндинг — профессор университета в Дерпте (ныне Тарту), — но не понял этого.

Доказательство логической непротиворечивости геометрии Лобачевского

Мы докажем непротиворечивость системы аксиом планиметрии Лобачевского, состоящей из четырех групп I1-3, II1-4, III1-5, IV1-2 аксиом Гильберта (аксиомы абсолютной планиметрии) и аксиомы V* Лобачевского. При решении этой задачи предполагается, что евклидова геометрия (т. е. система аксиом ∑H Гильберта) непротиворечива. Мы построим из объектов евклидовой плоскости модель плоскости Лобачевского, которая называется евклидовой моделью Кэли — Клейна. Рассмотрим на евклидовой плоскости некоторую окружность ω с центром О радиуса r = 1 и назовем ее абсолютом. Обозначим через Ω круг с границей ω, а через множество внутренних точек этого круга.

Введем следующие соглашения. Неевклидовой точкой назовем любую евклидову точку М, а неевклидовой прямой — любую хорду (без концов) окружности ω. Отношения «принадлежность» и «лежать между» понимаем в обычном смысле. Неевклидовы прямые будем обозначать так: UV, U1V1 и т. д., предполагая, что U, V, U1, V1 . Таким образом, неевклидовыми точками прямой UV будут те и только те евклидовы точки, которые лежат между точками U и V.

Нетрудно убедиться в том, что при этих соглашениях выполняются все аксиомы I1-3, II1-4 Гильберта. Проверим в качестве примера аксиому. Пусть А и В — две неевклидовы точки, a UV — неевклидова прямая, на которой они лежат. Так как А и В — внутренние точки хорды UV, то на этой хорде существует хотя бы одна внутренняя точка С, такая, что А — В — С. Отсюда мы заключаем, что существует по крайней мере одна неевклидова точка С, такая, что неевклидова точка В лежит между неевклидовыми точками А и С.

Так как в построенной модели выполняются все аксиомы групп I, II Гильберта, то выполняются и все следствия из этих аксиом, в частности имеют место теоремы, с помощью которых вводятся понятия луча и полуплоскости. Ясно, что неевклидовым лучом, исходящим из точки С, является множество всех внутренних точек произвольной полухорды CU окружности ω (CU — евклидов отрезок, где С — внутренняя точка круга Ω, a U — точка на его границе). Неевклидовой полуплоскостью является множество всех внутренних точек какого-нибудь сегмента круга Ω.

Для того чтобы в нашей модели определить равенство отрезков и углов, введем ряд вспомогательных понятий. Напомним, что на евклидовой плоскости простым отношением трех точек А, В и С, лежащих на одной прямой, называется число (АВ, С) = λ, такое, что , а сложным отношением четырех точек А, В, С, D, лежащих на одной прямой,— число (АВ, CD) = . Из этого определения непосредственно вытекают следующие свойства.

1. Если (АВ, CD) = (АВ, CD'), то точки D и D' совпадают.

2. Для любых четырех точек А, В, С, D прямой имеем (АВ, CD) = (CD, AB)= = (ВА, DC) = (DC, BA).

Если четыре точки на прямой заданы своими координатами M1(x1, у1), М2 (х2, y2), М3 (х3, у3) и M4 (х4, у4), то

. (1)

Одна из этих формул теряет смысл, если данные точки лежат на прямой, параллельной одной из координатных осей.

Биективное отображение f : Ω → Ω назовем -преобразованием, если выполнены следующие условия.

а) Внутренние точки круга Ω переходят во внутренние точки этого же круга, а граничные точки этого круга — в граничные точки.

б) Любая хорда окружности ω переходит в некоторую хорду этой же окружности, и при этом сохраняется сложное отношение соответственных точек.

Рассмотрим примеры -преобразований.

Пример 1. Любое движение евклидовой плоскости, имеющее центр абсолюта своей инвариантной точкой, индуцирует во множестве Ω некоторое -преобразование. В частности, тождественное преобразование множества Ω, вращение вокруг центра О круга Ω, отражение от любого диаметра круга Ω являются примерами -преобразований.

Пример 2. Пусть отображение f : Ω → Ω в системе координат Оху задано формулами

, ,где |a| < 1 (2)