Геометрия Лобачевского
Из равенства (3) следует, что точки абсолюта ω при отображении f переходят в точки абсолюта, а точки множества ![]() — в точки того же множества
— в точки того же множества ![]() . Далее, из равенств (4) мы заключаем, что каждая точка (х', у') множества Ω имеет единственный прообр
. Далее, из равенств (4) мы заключаем, что каждая точка (х', у') множества Ω имеет единственный прообр
аз (х, у), поэтому отображение (3) является биекцией множества Ω.
Отметим, что преобразование f, как показывают формулы (2) и (4), является инволютивным, т. е. f -1 = f.
Докажем, что для преобразования f выполняются также условия б). Если точки M1, M2,, M3 ![]() лежат на прямой Ах + By + С = 0, то, используя формулы (4), мы убеждаемся в том, что их образы M’1, M’2,, M’3
лежат на прямой Ах + By + С = 0, то, используя формулы (4), мы убеждаемся в том, что их образы M’1, M’2,, M’3 ![]() также лежат на некоторой прямой. Таким образом, если UV — некоторая хорда окружности ω, а U = f(U), V = f(V), то все точки хорды UV переходят в точки хорды U'V’. Но так как f -1 = f, то все точки хорды U'V’ переходят в точки хорды UV. Таким образом, хорда UV переходит в хорду U'V’.
также лежат на некоторой прямой. Таким образом, если UV — некоторая хорда окружности ω, а U = f(U), V = f(V), то все точки хорды UV переходят в точки хорды U'V’. Но так как f -1 = f, то все точки хорды U'V’ переходят в точки хорды UV. Таким образом, хорда UV переходит в хорду U'V’.
Остается доказать, что преобразование (2) сохраняет сложное отношение четырех точек. Пусть M1(x1, у1), М2 (х2, y2), М3 (х3, у3), M4 (х4, у4)— четыре точки, лежащие на одной прямой, пересекающей ось Оу, а М'i(хi, уi), i= 1, 2, 3, 4,— их образы. Используя первую из формул (4), находим:
![]()
где i , j = 1, 2, 3, 4, i ≠ j.
Отсюда, применяя формулу (1), получаем (М1М2, М3М4) = (М’1M’2, М'3M’4). Если точки Мi лежат на прямой, параллельной оси Оу. или на оси Оу, то используя вторую из формул (4), приходим к тому же выводу. Итак, доказано, что формулами (2) задано инволютивное ![]() -преобразование.
-преобразование.
Рассмотрим некоторые свойства ![]() -преобразований. Из определения
-преобразований. Из определения ![]() -преобразования непосредственно следует утверждение.
-преобразования непосредственно следует утверждение.
1°. Если f и g — ![]() -преобразования, то fg и f -1 являются
-преобразования, то fg и f -1 являются ![]() -преобразованиями.
-преобразованиями.
2°. Любое ![]() -преобразование сохраняет отношение «лежать между» точек круга Ω.
-преобразование сохраняет отношение «лежать между» точек круга Ω.
□ Пусгь А, В, С ![]() и А — В — С, а А', В', С' — образы этих точек. Обозначим через UV хорду, на которой лежат данные точки, а через U'V' образ этой хорды. Если точки А и С являются концами хорды UV (т. е. сов- падают с тачками U и V), то А' и С' являются концами хорды U'V'. В этом случае утверждение 2° очевидно. Предположим, что тачка U не совпадает ни с одной из точек А и С. Тогда (АС, ВU) = (А'С', B'U') или
и А — В — С, а А', В', С' — образы этих точек. Обозначим через UV хорду, на которой лежат данные точки, а через U'V' образ этой хорды. Если точки А и С являются концами хорды UV (т. е. сов- падают с тачками U и V), то А' и С' являются концами хорды U'V'. В этом случае утверждение 2° очевидно. Предположим, что тачка U не совпадает ни с одной из точек А и С. Тогда (АС, ВU) = (А'С', B'U') или ![]() . Так как (АС, V) < 0, (А'С', V') < 0 и по условию (АС, В) > 0, то из последнего равенства следует, что (А'С', В') > 0. Это означает, что А' — В' — С.
. Так как (АС, V) < 0, (А'С', V') < 0 и по условию (АС, В) > 0, то из последнего равенства следует, что (А'С', В') > 0. Это означает, что А' — В' — С.
Отсюда мы заключаем, что при ![]() -преобразовании отрезок, принадлежащий кругу Ω, переходит в отрезок; в частности, полухорда круга Ω переходит в полухорду того же круга. Далее, любой сегмент круга Ω переходит в сегмент того же круга.
-преобразовании отрезок, принадлежащий кругу Ω, переходит в отрезок; в частности, полухорда круга Ω переходит в полухорду того же круга. Далее, любой сегмент круга Ω переходит в сегмент того же круга.
Пусть UV - хорда круга Ω. AU — полухорда этой хорды, а ![]() — одни из сегментов, ограниченный хордой UV. Пару AU,
— одни из сегментов, ограниченный хордой UV. Пару AU, ![]() назовем
назовем ![]() -флагом и обозначим через (AU,
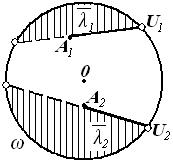
-флагом и обозначим через (AU, ![]() ). На рисунке 1 изображены два
). На рисунке 1 изображены два ![]() -флага (A1U1,
-флага (A1U1, ![]() ) и (A2U2 ,
) и (A2U2 , ![]() ). Из предыдущего ясно, что
). Из предыдущего ясно, что ![]() -преобразование любой
-преобразование любой ![]() -флаг переводит в
-флаг переводит в ![]() -флаг.
-флаг.
3. Какова бы ни была внутренняя точка А круга Ω. существует инволютивное ![]() -преобразование, которое переводит точку А в центр О круга Ω, а точку О в точку А.
-преобразование, которое переводит точку А в центр О круга Ω, а точку О в точку А.
□ В самом деле, пусть ОА = а. Выберем прямоугольную систему координат Оху так, чтобы точка А в этой системе имела координаты А(а, 0). Тогда -![]() преобразование, заданное формулами (2), переводит точку А в точку О, а точку О в точку А.
преобразование, заданное формулами (2), переводит точку А в точку О, а точку О в точку А.
4. Каковы бы ни были флаги I1 = (A1U1, ![]() ) и I2 = (A2U2,
) и I2 = (A2U2, ![]() ), существует
), существует ![]() -преобразование, которое I1 переводит в I2 (рис. 1).
-преобразование, которое I1 переводит в I2 (рис. 1).
□ По свойству 3° существуют инволютивные ![]() -преобразования f1 и f2, такие, что О = f1(A1) и О = f2(А2), где О - центр круга Ω. Пусть I1' = f1(I1) и I2' = f2(I2). Рассмотрим
-преобразования f1 и f2, такие, что О = f1(A1) и О = f2(А2), где О - центр круга Ω. Пусть I1' = f1(I1) и I2' = f2(I2). Рассмотрим ![]() -преобразование f0, такое, что I2' = f0(I1') (f0 является вращением вокруг точки О или вращением вокруг точки О с последующим отражением от диаметра круга Ω). Тогда f = f2f0f1 является искомым
-преобразование f0, такое, что I2' = f0(I1') (f0 является вращением вокруг точки О или вращением вокруг точки О с последующим отражением от диаметра круга Ω). Тогда f = f2f0f1 является искомым ![]() -преобразованием, так как f(I1) = f2f0f1(I1) = f2f0(I1 ') = f2(I2 ') = I2.
-преобразованием, так как f(I1) = f2f0f1(I1) = f2f0(I1 ') = f2(I2 ') = I2.
Отсюда получаем утверждение.
5°. Каковы бы ни были полухорды A1U1 и A2U2, существует ![]() -преобразование, которое полухорду A1U1 переводит в полухорду A2U2.
-преобразование, которое полухорду A1U1 переводит в полухорду A2U2.
6°. Если ![]() -преобразование какой-нибудь
-преобразование какой-нибудь ![]() -флаг переводит в себя, то оно является тождественным преобразованием круга Ω.
-флаг переводит в себя, то оно является тождественным преобразованием круга Ω.
В этом пункте для простоты изложения неевклидовы отрезки, лучи, углы, полуплоскости будем называть просто отрезками, лучами, углами, полуплоскостями. Введем следующие соглашения. Будем считать, что отрезок АВ ранен отрезку А'В', если существует такое ![]() -преобразование, которое отрезок АВ переводит в отрезок А'В'. Аналогично угол hk считается равным углу h'k', если существует
-преобразование, которое отрезок АВ переводит в отрезок А'В'. Аналогично угол hk считается равным углу h'k', если существует ![]() -преобразование f, которое угол hk переводит в угол h'k' (т. е. h' = f(h) и k' = f(k) или k' = f(h) и h' = f(k)).
-преобразование f, которое угол hk переводит в угол h'k' (т. е. h' = f(h) и k' = f(k) или k' = f(h) и h' = f(k)).
Другие рефераты на тему «Математика»:
- Статистическое исследование свойств псевдослучайных чисел получаемых методом Джона фон Неймана
- Решение военно-логистических задач по выбору оптимального маршрута для военно-транспортных средств
- Основы теории вероятности
- Методы статистического исследования
- Предельные теоремы. Характеристические функции
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
