Старший и верхний центральный показатели линейной системы

Для доказательства соотношения нам потребуется доказать несколько утверждений и следствий.

Утверждение 1.

Если семейство сужается, то его верхний класс может только расшириться, а верхнее число уменьшиться, то есть из

P’P

следует

8 height=29 src="images/referats/7469/image071.png">(P’)(P)

и

.

Доказательство.

Всякая верхняя функция для семейства P является верхней и для P’, так как P’P. Значит,

(P)(P’).

По определению 1.9

.

Из того, что

(P)(P’)

следует

.

А значит,

.

Утверждение 1 доказано.

Утверждение 2.

Если семейство P’ состоит из одной функции , то есть P’=, то верхнее среднее значение функции совпадает с верхним центральным числом семейства P’, то есть

Доказательство.

Для доказательства равенства

докажем два неравенства:

1) ;

2) .

1) Из определения 1.7 следует, что является верхней функцией, то есть

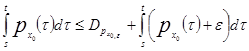, = 0;

итак,

(P’).

Следовательно, .

2) Пусть ─ любая верхняя функция семейства P’:

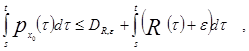
для любой (P’).

Тогда по определению 1.6

.

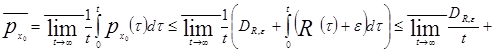
Так как ─ любое, то

для любой функции (P).

Следовательно,

.

Тем самым утверждение 2 доказано.

Следствие 1.(из утверждений 1 и 2)

Пусть P =─ семейство кусочно непрерывных функций и равномерно ограниченных функций. Тогда если семейство P’ состоит из одной функции , то есть P’=, и P’P , то верхнее среднее значение функции не превосходит верхнего центрального числа семейства P, то есть

.

Доказательство.

Так как P’P, то из утверждения 1 следует, что

(P’)(P)

и

.

Так как P’ состоит из одной функции, то есть P’= , то из утверждения 2 следует, что

.

Следовательно,

,

то есть

.

Следствие 1 доказано.

Следствие 2.(из следствия 1)

Пусть P = ─ семейство кусочно непрерывных и равномерно ограниченных функций. Тогда

.

Доказательство.

Из следствия 1 вытекает, что для любого выполняется

.

Следовательно,

.

Следствие 2 доказано.

Воспользуемся доказательством следствия 2 для доказательства следующего утверждения.

Утверждение 3.

Пусть ─

некоторая линейная система дифференциальных уравнений и

P = ─

семейство кусочно непрерывных и равномерно ограниченных функций, где

.

Тогда старший показатель Ляпунова не превосходит верхнего центрального числа семейства P, то есть

 Скачать реферат