Старший и верхний центральный показатели линейной системы

Вычислим .

По определению 1.6 верхнего среднего значения функции

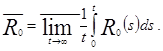
Для всякого найдется такое , что

.

Тогда

.

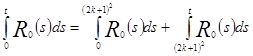Вычислим отдельно .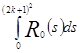

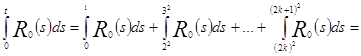
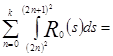
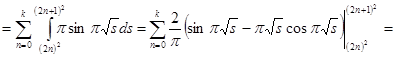
Итак,

.

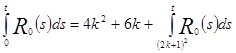Оценим сверху .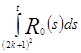

. (*)

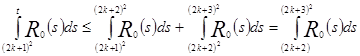Учитывая (*) и оценивая 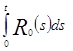сверху, получаем

.

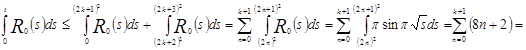
Тогда (при )

,

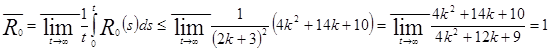то есть .

Оценивая 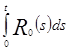снизу, получаем

,

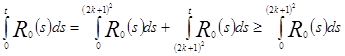где .

Тогда

,

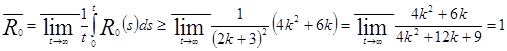то есть .

Следовательно, .

Теперь изобразим функции , и на графике.

График функции :

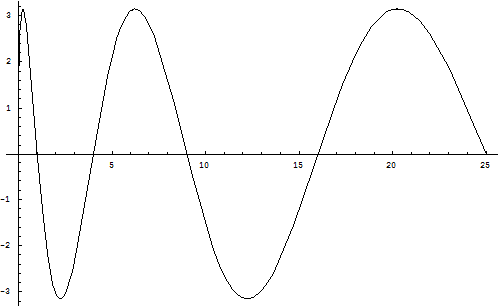
График функции :

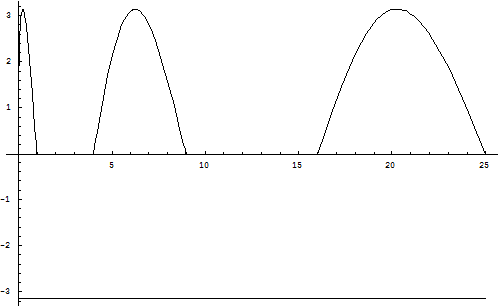
Очевидно, что на отрезках ,

а на отрезках для любого .

Теперь покажем, что верхний центральный показатель совпадает с , то есть

.

Докажем следующим образом:

1.Введем функцию .

Разобьем ось на промежутки точками

Используя определение 1.12, положим

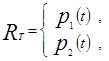если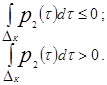

Оценим .

Возможны три случая:

1) если , то ; значит,

.

2) если , то ; значит,

.

2) если , то ; значит,

.

Таким образом, .

2.Докажем, что .

Очевидно, что ─ функция ограниченная и

.

Отсюда следует, что

,

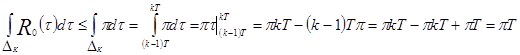то есть

,

Так как

,

то

.

3.Докажем, что для любого .

По определению 1.6 вычислим , используя утверждение 1.2:

.

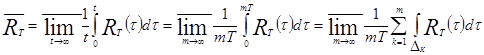По определению 1.6 вычислим , используя утверждение 1.2:

.

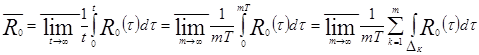Теперь рассмотрим все возможные случаи расположений отрезков по отношению к отрезкам и .

I. Если , где , то

,

следовательно,

;

 Скачать реферат