Линейные уравнения и их свойства

3. Проверить на уровне значимости нулевую гипотезу :при конкурирующей гипотезе : .

Задачу решить для следующих значений параметров , , .

Решение.1.Выборочное среднее при объеме выборки n=10 находится по формуле

.

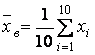Подставляя в формулу значения из таблицы 7, получим

=5,5 (%).

Для вычисления выборочной дисперсии используется формула

.

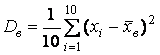Составим следующую вспомогательную таблицу, куда внесем отклонения и их квадраты .

Таблица 8

По данным таблицы 8 определим выборочное среднее

Выборочное среднее квадратическое отклонение находится:

Исправленную дисперсию находят для малых значений n (n<30) по значению :

Исправленное стандартное отклонение вычисляют путем извлечения квадратного корня из

:

Для оценки математического ожидания нормально распределенного признака по выборочной средней при неизвестном среднем квадратическом отклонении генеральной совокупности служит доверительный интервал

где =2,26 находим по таблице ([2], приложение 3) по заданным n=10 и =0,95.

Вычислим

Тогда

или

Оценкой среднего квадратического отклонения нормально распределенного количественного признака по исправленному выборочному среднему квадратическому отклонению служат доверительные интервалы

при

при

где находят по таблице ([2], приложение 4) по заданным значениям n=10 и =0,95. В данном случае и используется первая формула:

или

Чтобы найти вероятность того, что величина содержания крахмала в выбранной наудачу пробе окажется в пределе от до воспользуемся точечными оценками параметров нормального распределения и в формуле:

.

Учитывая нечетность функции Лапласа , имеем ([2], приложение 2)

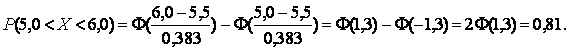
3. Для того, чтобы при заданном уровне значимости , проверить нулевую гипотезу : о равенстве неизвестной генеральной средней гипотетическому значению при конкурирующей гипотезе : , надо вычислить наблюдаемое значение статистического критерия

 Скачать реферат