Линейные уравнения и их свойства

Наконец, после подстановки найденных значений в первое уравнение, находим неизвестную : Таким образом, решение системы единственное:

Пример 3. Решить систему уравнений

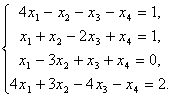(7)

Решение. Запишем и преобразуем расширенную матрицу системы (7)

~ ~

~~ ~

~ ~ .

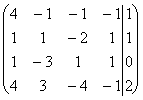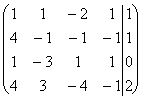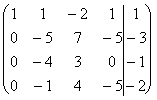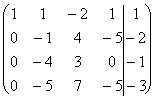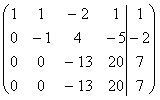Расширенная матрица, полученная на последнем шаге путем вычитания из элементов четвертой строки соответствующих элементов третьей строки, содержит нулевую строку и имеет ступенчатый вид. Отсюда следует, что исходной системе уравнений эквивалентна система из трех уравнений с 4 неизвестными

Неизвестную перенесем в правые части уравнений

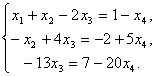
Отсюда определяем

Задавая переменной произвольное значение , найдем бесконечное множество решений системы

Если расширенная матрица системы приведена к ступенчатому виду, когда в нулевой строке основной матрицы свободный член отличен от нуля, то система не имеет решения. Например, последняя строка имеет вид . Тогда соответствующее уравнение системы привелось к неверному равенству

Пример 4. Предприятие выпускает три вида товаров, при производстве которых используется три типа ресурсов: рабочая сила, сырье, оборудование. Нормы расхода каждого из них (в условных единицах) на производство единицы каждого товара и объем ресурсов на 1 день заданы таблицей 1.

Таблица 1

Найти ежедневный объем выпуска каждого товара.

Решение. Пусть - ежедневный выпуск соответственно товаров 1,2 и 3-го вида. Тогда в соответствии с нормами расхода ресурсов каждого типа имеем систему линейных уравнений, содержащих неизвестные

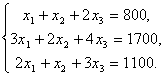
Решим ее методом Гаусса.

~ ~

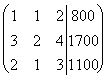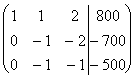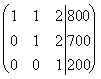
Отсюда находим , т.е. предприятие ежедневно выпускает 100 ед. товаров 1-го вида, 300 ед. товаров 2-го вида и 200 ед. товаров 3-го вида.

Задача для контрольной работы

Кондитерская фабрика специализируется на выпуске изделий трех видов. При этом используется сырье трех типов. Нормы расхода каждого из них на одно изделие и общий объем расхода сырья на 1 день заданы таблицей 2. Найти ежедневный объем выпуска каждого вида изделия, построив систему линейных уравнений и решая ее методом Гаусса и по формулам Крамера.

Таблица 2

 Скачать реферат