Линейные уравнения и их свойства

которое можно записать для соответствующих координат этих векторов

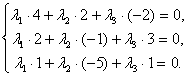(3)

Решим полученную систему линейных уравнений (3) методом Гаусса.

~ ~ ~

~~ ~ ~

~~ .

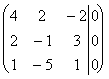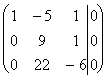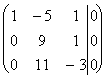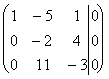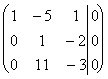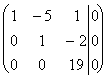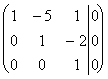Отсюда получаем единственное нулевое решение , т.е. векторы являются линейно независимыми и, следовательно, образуют базис пространства. Найдем теперь разложение вектора по базису из условия выполнения векторного равенства

,

которое для соответствующих координат запишется

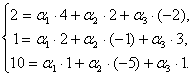
Полученную квадратную систему линейных уравнений относительно неизвестных решим по формулам Крамера. Вычислим определители3-го порядка:

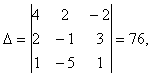
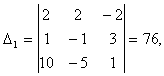
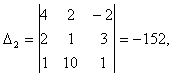
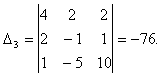
Тогда по формулам Крамера находим координаты вектора в базисе :

В итоге имеем

Задача для контрольной работы

Показать, что векторы образуют базис и найти координаты вектора в этом базисе. Численные данные в зависимости от варианта приводятся в таблице 3.

Таблица 3

 Скачать реферат