Построение эйлерова цикла. Алгоритм Форда и Уоршелла

1. Эйлеровы цепи и циклы

Рассматриваемая задача является одной из самых ста­рей­ших в теории графов. В городе Кенигсберге (ныне Калининград) имелось семь мостов, соединяющих два берега реки Преголь, и два основа на ней друг с другом (рис. 1а). Требуется, начав путешествие из одной точки города прой­ти по всем мостам по одному разу и вернуться в исходную точку.

=491 height=144 src="images/referats/3106/image001.png">

а) б)

Рис. 1.

Если поставить в соответствие мостам ребра, а участкам суши — вершины, то получится граф (точнее псевдограф), в котором надо найти про­стой цикл, проходящий через все ребра. В общем виде эта задача была решена Эйлером в 1736 г.

Определение 1. Эйлеровой цепью в неориентированном графе G называется простая цепь, содержащая все ребра графа G. Эйлеровым циклом назы­вается замкнутая Эйлерова цепь. Аналогично, эйлеров путь в орграфе G — это простой путь, содержащий все дуги графа G. Эйлеров контур в орграфе G — это замкнутый эйлеров путь. Граф, в котором существует эйлеров цикл, называется эйлеровым.

Простой критерий существования эйлерова цикла в связном графе дается следующей теоремой.

Теорема 1. (Эйлер) Эйлеров цикл в связном неориентированном графе G(X, E) существует только тогда, когда все его вершины имеют четную степень.

Доказательство. Необходимость. Пусть m - эйлеров цикл в связном гра­фе G, x — произвольная вершина этого графа. Через вершину x эйлеров цикл проходит некоторое количество k (k³1) раз, причем каждое прохождение, очевидно, включает два ребра, и степень этой вершины равна 2k, т.е. четна, так как x выбрана произвольно, то все вершины в графе G имеют четную сте­пень.

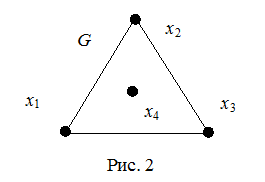
Достаточность. Воспользуемся индукцией по числу m ребер графа. Эйле­ровы циклы для обычных (не псевдо) графов можно построить начиная с m=3.Легко проверить, что единственный граф с m=3, имеющий все вершины с четными степенями, есть граф K3 (рис. 2). Существование эйлерова цикла в нем очевидно. Таким образом, для m=3 достаточность условий доказываемой теоремы имеет место. Пусть теперь граф G имеет m>3 ребер, и пусть утверждение справедливо для всех связных графов, имеющих меньше, чем m ребер. Зафиксируем произвольную вершину a графа G и будем искать простой цикл, идущий из a в a. Пусть m(a, x) — простая цепь, иду­щая из a в некоторую вершину x. Если x ¹ a, то цепь m можно продолжить из вершины x в некотором направлении. Через некоторое число таких про­дол­­же­ний мы придем в вершину zÎX, из которой нельзя продлить полу­чен­ную про­стую цепь. Легко видеть, что z = a так как из всех остальных вершин цепь может выйти (четные степени!); a в a она начиналась. Таким образом, нами построен цикл m, идущий из a в a. Предположим, что построенный про­стой цикл не содержит всех ребер графа G. Удалим ребра, входящие в цикл m, из графа G и рассмотрим полученный граф . В графе все вершины имеют четные степени. Пусть — компо­нен­ты связ­нос­ти графа , содержащие хотя бы по одному ребру. Соглас­но пред­поло­же­нию индукции все эти компоненты обладают эйлеровыми циклами m1, m1, …, mkсоот­вет­ствен­но. Так как граф G связан, то цепь m встре­чает каждую из компонент. Пусть первые встречи цикла m с ком­понентами происходят соответственно в вершинах x1, x2, …, xk. Тогда про­стая цепь

n(a, a)=m(a, x1) U m1(x1, x1) U m(x1, x2) U…U mk(xk, xk) U m(xk, a)

является эйлеровым циклом в графе G. Теорема доказана.

Замечание. Очевидно, что приведенное доказательство будет верно и для псевдографов, содержащих петли и кратные ребра (см. рис. 1,а).

Таким образом, задача о кенигсбергских мостах не имеет ре­ше­ния, так как соответствующий граф (см. рис. 1,б) не имеет эйлерова цикла из-за не­четности степеней все вершин.

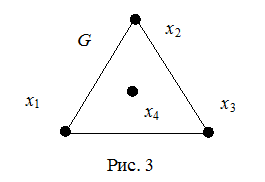Отметим, что из существования эйле­ро­ва цикла в неориентированном графе G не следует связность этого графа. Напри­мер, неориентированный граф G на рис. 3 обладает эйлеровым циклом и вместе с тем несвязен.

Совершенно также, как теорема 1, могут быть доказаны следующие два утверждения.

Теорема 2. Связный неориентированный граф G обладает эйлеровой цепью тогда и только тогда, когда число вершин нечетной степени в нем равно 0 или 2, причем если это число равно нулю, то эйлерова цепь будет являться и циклом.

Теорема 3. Сильно связный орграф G(X, E) обладает эйлеровым кон­ту­ром тогда и только тогда, когда для любой вершины xÎX выполняется

.

Можно также обобщить задачу, которую решал Эйлер следующим обра­зом. Будем говорить что множество не пересекающихся по ребрам простых цепей графа G покрывает его, если все ребра графа G включены в цепи mi. Нужно найти наименьшее количество таких цепей, которыми можно покрыть заданный граф G.

Если граф G — эйлеров, то очевидно, что это число равно 1. Пусть теперь G не является эйлеровым графом. Обозначим через k число его вер­шин нечетной степени. По теореме … k четно. Очевидно, что каждая верши­на нечетной степени должна быть концом хотя бы одной из покрывающих G цепей mi. Следовательно, таких цепей будет не менее чем k/2. С другой сто­роны, таким количеством цепей граф G покрыть можно. Чтобы убедиться в этом, расширим G до нового графа , добавив k/2 ребер , соединяющих раз­личные пары вершин нечетной степени. Тогда оказывается эйлеровым графом и имеет эйлеров цикл . После удаления из ребер граф разло­жится на k/2 цепей, покрывающих G. Таким образом, доказана.

Теорема 4. Пусть G — связный граф с k>0 вершинами нечетной степени. Тогда минимальное число непересекающихся по ребрам простых цепей, покрывающих G, равно k/2.

Алгоритм построения эйлерова цикла

Для начала отметим, что теорема 1 также дает метод построения эйлерова цикла. Здесь мы рассмотрим несколько иной алгоритм.

Пусть G(X, E) — связный неорентированный граф, не имеющий вершин нечетной степени. Назовем мостом такое ребро, удаление которого из связного графа разбивает этот граф на две компоненты связности, имеющие хотя бы по одному ребру.

 Скачать реферат