Интеграл Лебега-Стилтьеса
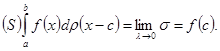 (13)
(13)
Аналогично можно убедиться в том, что (при ![]() )
)
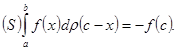 (14)
(14)
(при ![]() этот интеграл обращается в нуль).
этот интеграл обращается в нуль).
Теперь мы в состоянии доказат
ь теорему, в некотором смысле более общую, чем 2, а именно, отказаться от требования непрерывности функции:
Пусть функция ![]() в промежутке
в промежутке ![]() непрерывна, а
непрерывна, а ![]() имеет в этом промежутке, исключая разве лишь конечное число точек, производную
имеет в этом промежутке, исключая разве лишь конечное число точек, производную ![]() , которая абсолютно интегрируема в
, которая абсолютно интегрируема в ![]() . При этом пусть функция
. При этом пусть функция ![]() в конечном числе точек
в конечном числе точек
![]()
терпит разрыв первого рода. Тогда существует интеграл Стилтьеса и выражается формулой
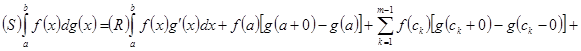
![]() (15)
(15)
Характерно здесь наличие внеинтегральной суммы, где фигурируют скачки функции ![]() в точках
в точках ![]() или
или ![]() - односторонние.
- односторонние.
Для упрощения записи введем обозначения для скачков функции ![]() справа и слева:
справа и слева:
![]()
![]()
очевидно, для
![]()
![]()
Составим вспомогательную функцию:
![]()
которая как бы вбирает в себя все разрывы функции ![]() , так что разность
, так что разность ![]() , как мы сейчас установим, оказывается уже непрерывной.
, как мы сейчас установим, оказывается уже непрерывной.
Для значений ![]() , отличных от всех
, отличных от всех ![]() , непрерывность функции
, непрерывность функции ![]() не вызывает сомнений, ибо для этих значений непрерывны обе функции
не вызывает сомнений, ибо для этих значений непрерывны обе функции ![]() и
и ![]() . Докажем теперь непрерывность
. Докажем теперь непрерывность ![]() в точке
в точке ![]() справа. Все слагаемые суммы
справа. Все слагаемые суммы ![]() , кроме члена
, кроме члена ![]() , непрерывны при
, непрерывны при ![]() справа; поэтому достаточно изучить поведение выражения
справа; поэтому достаточно изучить поведение выражения ![]() . При
. При ![]() оно имеет значение
оно имеет значение ![]() ; но таков же и его предел при
; но таков же и его предел при ![]() :
:
![]()
Аналогично проверяется и непрерывность функции ![]() в точке
в точке ![]() слева.
слева.
Далее, если взять точку ![]() (отличную от всех
(отличную от всех ![]() ), в которой функция
), в которой функция ![]() имеет производную, то вблизи этой точки
имеет производную, то вблизи этой точки ![]() сохраняет постоянное значение, следовательно, в ней и функция
сохраняет постоянное значение, следовательно, в ней и функция ![]() имеет производную, причем
имеет производную, причем
![]() .
.
Для непрерывной функции ![]() , по предыдущей теореме, существует интеграл Стилтьеса
, по предыдущей теореме, существует интеграл Стилтьеса
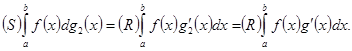
Точно так же легко вычислить и интеграл
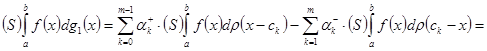
![]()
![]()
Складывая почленно эти два равенства, мы и придем к равенству (15); существование интеграла Стилтьеса от ![]() по функции
по функции ![]() устанавливается попутно (п.4,3).
устанавливается попутно (п.4,3).
2.8 Примеры
Вычислить по формуле (11) интегралы:
а) 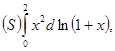
б) 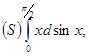
в) ![]()
Решение:
а) 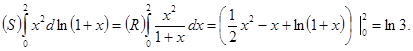
б) ![]()
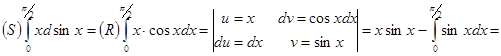
![]()
в) ![]()
Вычислить по формуле (15) интегралы:
а) ![]() где
где 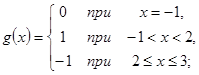
б) 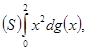 где
где 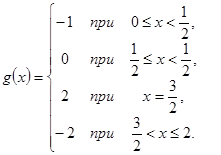
Решение:
а) Функция ![]() имеет скачок 1 при
имеет скачок 1 при ![]() и скачок - 2 при
и скачок - 2 при ![]() ; в остальных точках
; в остальных точках ![]() . Поэтому
. Поэтому
![]()
б) Скачок 1 при ![]() и - 2 при
и - 2 при ![]() (значение функции
(значение функции ![]() при
при ![]() не влияет на результат); в прочих точках
не влияет на результат); в прочих точках ![]() .
.
Другие рефераты на тему «Математика»:
- Структурные особенности учебного материала в школьном курсе геометрии
- Решение систем дифференциальных уравнений при помощи неявной схемы Адамса 3-го порядка
- Числовые характеристики случайной функции и выборочная функция распределения
- Метод конечных разностей или метод сеток
- Теорема Бернулли. Закон распределения Пуассона. Критерий Колмогорова
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
