Интеграл Лебега-Стилтьеса

В первой теореме о предельном переходе под знаком интеграла Стилтьеса мы поставили требование, чтобы последовательность функций стремилась к предельной функции равномерно. Можно, однако, заменить это требование более общим условием, что эти функции ограничены в их сово

купности:

(Только при этом нужно ещё наперед предположить непрерывность предельной функции ).

При доказательстве достаточно рассмотреть случай, когда возрастает в строгом смысле. Но для этого случая можно воспользоваться преобразованием, проведенным в п.:

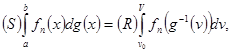
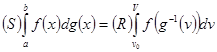
и, имея дело уже с римановыми интегралами, просто применить теорему Арцелла.

Укажем, в заключение, другую трактовку понятия интеграла Стилтьеса, связав его с понятием аддитивной функции от промежутка.

Пусть для каждой части данного промежутка определено число , причем, если промежуток точкой разложен на части и , то и

Тогда есть аддитивная функция от переменного промежутка . Предположим, что кроме неё для промежутка задана и функция точки . Разложим теперь, как обычно, промежуток точками

на части , в каждой части произвольно выберем по точке и, наконец, составим сумму

(32)

Предел этой суммы при и есть интеграл Стилтьеса, который естественно - учитывая процесс его построения - обозначить так:

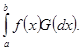(33)

Если определить вторую функцию точки , положив

для

то, ввиду аддитивности функции , во всех случаях

(34)

так что сумма (32) сведется к обыкновенной стилтьесовой сумме

а предел (33) - к обыкновенному интегралу Стилтьеса

.

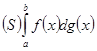Обратно, если существует последний интеграл, то, определив функцию от промежутка равенством (34) (причем легко проверить, что она окажется аддитивной), можно свести обыкновенный интеграл Стилтьеса к интегралу (33).

Глава III. Применение интеграла Стилтьеса

3.1 Применение в теории вероятностей

В элементарной теории вероятностей, где рассматриваются случайные величины , которые могут принимать только конечное множество значений , среднее значение или математическое ожидание определяется формулой:

(1)

Имея эту формулу, мы можем при помощи интеграла Стилтьеса распространить определение среднего значения на случайные величины , которые могут принимать любое множество значений, заключенное в каком-нибудь ограниченном интервале , - если только мы примем следующую аксиому:

Каковы бы ни были функции и случайной величины , для которых всегда , для них будут иметь место также и неравенства:

(2)

Чтобы распространить определения среднего значения, возьмем какое-нибудь подразделение

и пусть и , когда Здесь , и поэтому в силу условия (2):

Величины же и , таким образом определенные, могут принимать соответственно только значения и , а потому по формуле (1):

С другой стороны, очевидно, что вероятности и обе равны вероятности , и потому

Итак, если ввести функции распределения случайной величины :

 Скачать реферат