Интеграл Лебега-Стилтьеса
![]()
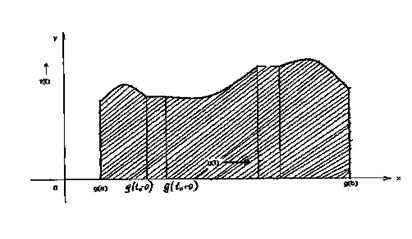
Геометрическая иллюстрация интеграла Стилтьеса
Рассмотрим интеграл
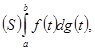 (20)
(20)
предполагая функцию ![]() непрерывной интеграл пол
непрерывной интеграл пол
ожительной, а ![]() - лишь монотонно возрастающей (в строгом смысле); функция
- лишь монотонно возрастающей (в строгом смысле); функция ![]() может иметь и разрывы (скачки).
может иметь и разрывы (скачки).
Система параметрических уравнений
![]() (21)
(21)
выражает некоторую кривую ![]() , вообще говоря, разрывную (рис). Если при некотором
, вообще говоря, разрывную (рис). Если при некотором ![]() функция
функция ![]() испытывает скачок, так что
испытывает скачок, так что ![]() , то этим предельным значениям
, то этим предельным значениям ![]() отвечает одно интеграл то же предельное значение
отвечает одно интеграл то же предельное значение ![]() , равное
, равное ![]() . Дополним кривую
. Дополним кривую ![]() всеми горизонтальными отрезками, соединяющими пары точек
всеми горизонтальными отрезками, соединяющими пары точек
![]()
![]() и
и ![]()
отвечающие всем скачкам функции ![]() (см. рис). Таким образом, составится уже непрерывная кривая
(см. рис). Таким образом, составится уже непрерывная кривая ![]() . Покажем, что интеграл (20) представляет площадь фигуры под этой кривой, точнее, площадь фигуры, ограниченной кривой
. Покажем, что интеграл (20) представляет площадь фигуры под этой кривой, точнее, площадь фигуры, ограниченной кривой ![]() , осью и двумя крайними ординатами, отвечающими абсциссам
, осью и двумя крайними ординатами, отвечающими абсциссам ![]() и
и ![]() .
.
С этой целью разложим промежуток на части точками
![]()
и в соответствии с этим промежуток ![]() на оси
на оси ![]() - на части точками
- на части точками
![]()
Введя наименьшее и наибольшее значения ![]() и
и ![]() функции
функции ![]() в
в ![]() -м промежутке
-м промежутке ![]() , составим нижнюю интеграл верхнюю суммы Стилтьеса-Дарбу
, составим нижнюю интеграл верхнюю суммы Стилтьеса-Дарбу
![]()
Легко видеть теперь, что они представляют площади фигур, составленных из входящих интеграл из выходящих прямоугольников, между которыми содержится рассматриваемая криволинейная фигура.
Так как при стремлении к 0 всех ![]() обе суммы стремятся к общему пределу (20), то отсюда следует, что наша фигура квадрируема и площадью её служит действительно интеграл (20).
обе суммы стремятся к общему пределу (20), то отсюда следует, что наша фигура квадрируема и площадью её служит действительно интеграл (20).
2.10 Теорема о среднем, оценки
Пусть в промежутке ![]() функция
функция ![]() ограничена:
ограничена:
![]()
а ![]() монотонно возрастает. Если существует интеграл Стилтьеса
монотонно возрастает. Если существует интеграл Стилтьеса ![]() от
от ![]() по
по ![]() , то имеет место формула
, то имеет место формула
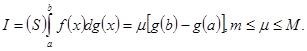 (22)
(22)
Это и есть теорема о среднем для интегралов Стилтьеса.
Для доказательства будем исходить из очевидных неравенств для стилтьесовской суммы ![]() :
:
![]()
Переходя к пределу, получим
![]() (23)
(23)
Или
![]()
Обозначая написанное отношение через ![]() , придем к (22).
, придем к (22).
Если функция ![]() в промежутке
в промежутке ![]() непрерывна, то обычным путем убеждаемся в том, что
непрерывна, то обычным путем убеждаемся в том, что ![]() есть значение функции в некоторой точке этого промежутка, интеграл формула (22) приобретает вид
есть значение функции в некоторой точке этого промежутка, интеграл формула (22) приобретает вид
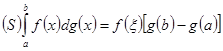 , где
, где ![]() (24)
(24)
В практике интегралов Стилтьеса наиболее важным является случай, когда функция ![]() непрерывна, а функция
непрерывна, а функция ![]() имеет ограниченное изменение. Для этого случая справедлива такая оценка интеграла Стилтьеса:
имеет ограниченное изменение. Для этого случая справедлива такая оценка интеграла Стилтьеса:
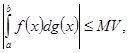 (25)
(25)
Где
![]() .
.
Действительно, для суммы Стилтьеса ![]() будет
будет
![]()
так что остается лишь перейти к пределу, чтобы получить требуемое неравенство.
Отсюда вытекает, в частности, и оценка близости суммы ![]() к самому интегралу Стилтьеса
к самому интегралу Стилтьеса ![]() (при прежних предположениях относительно функций
(при прежних предположениях относительно функций ![]() и
и ![]() ). Представив
). Представив ![]() и
и ![]() в виде
в виде
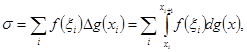
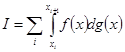
и почленно вычитая эти равенства, получим
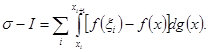
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
