Интеграл Лебега-Стилтьеса
то интеграл (5) существует.
Для того чтобы опять иметь возможность применить установленный выше критерий, предположим сначала функцию ![]() не только удовлетворяющей условию (6), но и монотонно возрастающей.
не только удовлетворяющей условию (6), но и монотонно возрастающей.
Ввиду (6), очевидно, ![]() , так что
, так что
src="images/referats/3141/image152.png">.
Но последняя сумма при ![]() и сама стремится к 0 вследствие интегрируемости (в смысле Римана) функции
и сама стремится к 0 вследствие интегрируемости (в смысле Римана) функции ![]() , а тогда стремится к нулю и первая сумма, что доказывает существование интеграла (5).
, а тогда стремится к нулю и первая сумма, что доказывает существование интеграла (5).
В общем случае функции ![]() , удовлетворяющей условию Липшица (6), представим в виде разности
, удовлетворяющей условию Липшица (6), представим в виде разности
![]()
Функция ![]() , очевидно, удовлетворяет условию Липшица и в то же время монотонно возрастает. То же справедливо и для функции
, очевидно, удовлетворяет условию Липшица и в то же время монотонно возрастает. То же справедливо и для функции ![]() , так как, в силу (6), при
, так как, в силу (6), при ![]()
![]()
и
![]()
В таком случае рассуждение завершается, как и выше.
III. Если функция ![]() интегрируема в смысле Римана, а функция
интегрируема в смысле Римана, а функция ![]() представима в виде интеграла с переменным верхним пределом:
представима в виде интеграла с переменным верхним пределом:
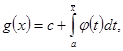 (7)
(7)
где ![]() абсолютно интегрируема, в промежутке
абсолютно интегрируема, в промежутке ![]() , то интеграл (5) существует.
, то интеграл (5) существует.
Пусть ![]() , так что
, так что ![]() монотонно возрастает. Если
монотонно возрастает. Если ![]() интегрируема в собственном смысле и, следовательно, ограничена:
интегрируема в собственном смысле и, следовательно, ограничена: ![]() то для
то для ![]()
Имеем
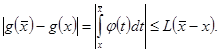
Таким образом, в этом случае ![]() удовлетворяет условию Липшица, и интеграл существует в силу 2.
удовлетворяет условию Липшица, и интеграл существует в силу 2.
Предположим теперь, что ![]() интегрируема в несобственном смысле. Ограничимся случаем одной особой точки, скажем
интегрируема в несобственном смысле. Ограничимся случаем одной особой точки, скажем ![]() . Прежде всего, по произвольно взятому
. Прежде всего, по произвольно взятому ![]() выберем
выберем ![]() так, чтобы было
так, чтобы было
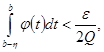 (8)
(8)
где ![]() - общее колебание функции
- общее колебание функции ![]() в рассматриваемом промежутке.
в рассматриваемом промежутке.
Разобьем промежуток ![]() по произволу на части и составим сумму
по произволу на части и составим сумму
![]()
Она разлагается на две суммы ![]() , из коих первая отвечает промежуткам, целиком содержащимся в промежутке
, из коих первая отвечает промежуткам, целиком содержащимся в промежутке ![]() , а вторая - остальным промежуткам. Последние наверное содержаться в промежутке
, а вторая - остальным промежуткам. Последние наверное содержаться в промежутке ![]() , если только
, если только ![]() ; тогда, в силу (8),
; тогда, в силу (8),
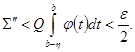
С другой стороны, так как в промежутке ![]() функция
функция ![]() интегрируема в собственном смысле, то по доказанному при достаточно малом
интегрируема в собственном смысле, то по доказанному при достаточно малом ![]() и сумма
и сумма ![]() станет меньше
станет меньше ![]() . Отсюда следует (4), что и требовалось доказать.
. Отсюда следует (4), что и требовалось доказать.
В общем случае, когда функция ![]() абсолютно интегрируема в промежутке
абсолютно интегрируема в промежутке ![]() , мы рассмотрим функции
, мы рассмотрим функции
![]()
очевидно, неотрицательные и интегрируемые в названном промежутке. Так как
![]()
то вопрос сводится, как и выше, к уже рассмотренному случаю.
Замечание. Пусть функция ![]() непрерывна в промежутке
непрерывна в промежутке ![]() и имеет, исключая разве лишь конечное число точек, производную
и имеет, исключая разве лишь конечное число точек, производную ![]() , причем эта производная интегрируема (в собственном или несобственном смысле) от
, причем эта производная интегрируема (в собственном или несобственном смысле) от ![]() до
до ![]() ; тогда, как известно, имеет место формула типа (7):
; тогда, как известно, имеет место формула типа (7):
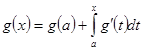 .
.
Если ![]() абсолютно интегрируема, то к функции
абсолютно интегрируема, то к функции ![]() полностью приложимо изложенное в 3.
полностью приложимо изложенное в 3.
2.4 Свойства интеграла Стилтьеса
Из определения интеграла Стилтьеса непосредственно вытекают следующие его свойства:
![]()
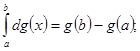
![]()
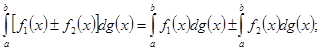
![]()
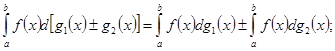
![]()
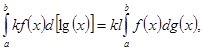
![]()
При этом в случаях ![]() из существования интегралов в правой части вытекает существование интеграла в левой части.
из существования интегралов в правой части вытекает существование интеграла в левой части.
Затем имеем
![]()
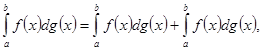
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
