Моделирование рабочих процессов погрузочно-транспортных модулей с учетом случайного характера внешних воздействий

Другой проверкой адекватности раздельного моделирования заполнения ёмкости v как независимого числа кусков каждого разряда является выполнение условия:

.

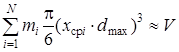Изменение гранулометрического состава исходного штабеля после очередного черпания производится в следующем порядке:

1) вычисляется суммарный объём выгруженного матер

иала из штабеля после каждого j-го черпания:

;

2) находится остаточный объём штабеля после j-го черпания:

Vj = Vj-1 – VΣ;

3) определяется новое долевое содержание каждой фракции i (xcpi) к началу (j+1)-го черпания:

.

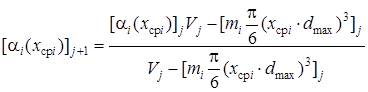Таким образом, формируется новый гранулометрический состав штабеля как функция [i (xcpi)]k, где k = 1, 2,….,j, j+1, … k, k – число черпаний ковшом из штабеля. Для каждого последующего состояния штабеля должно соблюдаться соотношение:

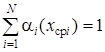. (2.2)

Так как моделирование числа кусков и, следовательно, долевое содержание каждого разряда производится независимо от других разрядов размеров куска xcpi, то возможно нарушение последнего условия. В целях проверки выполнения условия (2.2) проведены численные эксперименты по выгрузке штабеля V = 30 м3 ковшом со средним наполнением v = 0,9 м3. Штабель в начальном состоянии содержит NN = 10 фракций, dmax = 0,57 м, гранулометрический состав i (xcpi) представлен в таблице 2.1.

Численное моделирование для «черпаний» с возвратом горной массы в штабель выполнялись для ранее указанных исходных данных рядового штабеля (тип функции распределения – F4(x) – рис. 2.2), шаг изменения крупности по разрядам – ∆ = 0,06 м. Исходные данные, программа моделирования в среде MathCad [98] и основные результаты приведены в приложении 1.

Таблица 2.1

Исходный относительный долевой состав штабеля по объёму и математическое ожидание числа кусков в ковше

В каждом разряде i независимо друг от друга с помощью датчиков случайных чисел генерируется число кусков mi, i Î (0, ni) с вероятностью по биноминальному закону распределения (2.1). Среднее значение совокупности чисел mi, выпавших в каждом разряде, должно стремиться к величине ni i.

Реальное число кусков, попадающих в объём v по каждому i-му разряду Nnкi,j в j-м цикле «черпания», является случайной величиной, числовые характеристики которой зависят от исходного гранулометрического состава штабеля F(xi), соотношения объёмов штабеля и ковша V/v, размеров кусков. При моделировании результаты формировались в следующем виде:

- матрица Nnкi,j – число кусков j-го разряда, попавших в ковш после каждого j-го цикла черпания;

- матрица Vкi,j – объём фракций j-го разряда, попавших в ковш после каждого j-го цикла черпания;

- матрица Ркi,j – долевое содержание i-й фракции после j-го цикла черпания.

Отдельные реализации величины i = Ркi,j на фоне математического ожидания аналогичной величины в штабеле показаны на рисунке 2.4. Программа и результаты моделирования приведены в приложении 1.

Оценка достоверности результатов моделирования проводилась сравнением величин:

а) суммарного объёма материала, попавшего во фракции в процессе моделирования в каждом i-м цикле 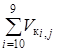с номинальным объёмом ковша v;

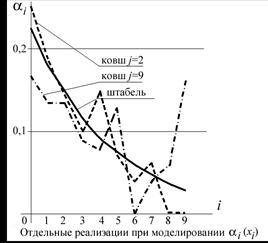
Рис. 2.4. Результаты отдельной реализации гранулометрического состава в малом выделенном объёме

б) среднего значения долевого участия каждой фракции по всем циклам моделирования 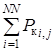c долевым участием соответствующей фракции в объёме штабеля i.

Результаты сравнения приводятся в таблицах 2.2 и 2.3. Обозначено:

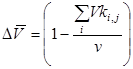, × 100 %, 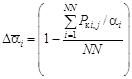× 100 %.

Анализ результатов численного моделирования показывает, что суммарный объём материала, аккумулирующийся в малой выделенной ёмкости во многих «черпаниях», существенно отличается от величины v.

 Скачать реферат