Определенный интеграл

.

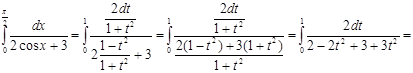
Пример 5. Вычислить интеграл .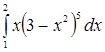

Решение. Положим , тогда , откуда . Находим новые пределы интегрирования: ; . Имеем: . Следовательно:

.

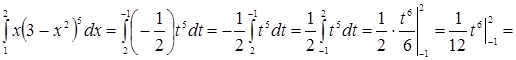
6. Интегрирование по частям

Теорема 4. Пусть функции и имеют непрерывные производные на отрезке . Тогда имеет место следующая формула интегрирования по частям:

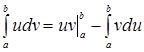. (4)

Доказательство

Так как , то функция является первообразной для функции . Тогда по формуле Ньютона–Лейбница получаем

,

откуда

.

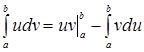Пример 6. Вычислить .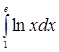

Решение. Положим , отсюда . По формуле (4) находим

.

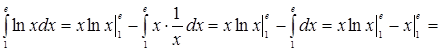
Пример 7. Вычислить .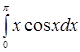

Решение. Пусть , тогда . Применяя формулу интегрирования по частям, получаем

.

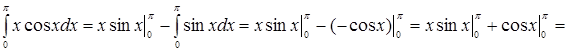
Пример 8. Вычислить .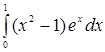

Решение. Полагая , определяем . Следовательно:

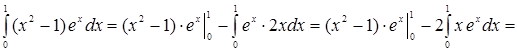
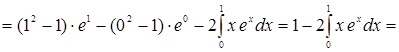[к полученному интегра-лу снова применяем формулу интегрирования по частям: ; следовательно: ] = =

.

Лекция 2. Применение определенных интегралов. Несобственные интегралы

1. Площадь криволинейной трапеции

Пусть функция неотрицательна и непрерывна на отрезке . Тогда, согласно геометрическому смыслу определенного интеграла, площадь криволинейной трапеции, ограниченной сверху графиком этой функции, снизу – осью , слева и справа – прямыми и (см. рис. 2) вычисляется по формуле

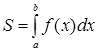. (5)

Пример 9. Найти площадь фигуры, ограниченной линией и осью .

Решение. Графиком функции является парабола, ветви которой направлены вниз. Построим ее (рис. 3). Чтобы определить пределы интегрирования, найдем точки пересечения линии (параболы) с осью (прямой ). Для этого решаем систему уравнений

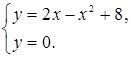
Получаем: , откуда , ; следовательно, , .

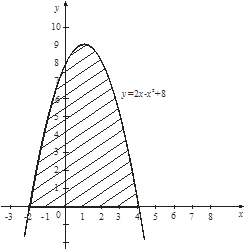
Рис. 3

Площадь фигуры находим по формуле (5):

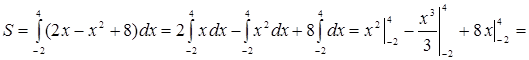
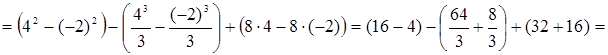
(кв. ед.).

Если функция неположительна и непрерывна на отрезке , то площадь криволинейной трапеции, ограниченной снизу графиком данной функции, сверху – осью , слева и справа – прямыми и , вычисляется по формуле

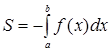. (6)

В случае если функция непрерывна на отрезке и меняет знак в конечном числе точек, то площадь заштрихованной фигуры (рис. 4) равна алгебраической сумме соответствующих определенных интегралов:

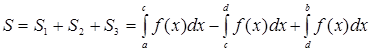. (7)

Рис. 4

Пример 10. Вычислить площадь фигуры, ограниченной осью и графиком функции при .

 Скачать реферат