Определенный интеграл
Из условия задачи следует, что ![]() ,
, ![]() . По формуле (9) получаем
. По формуле (9) получаем
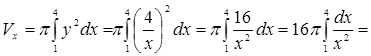
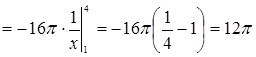 .
.

Рис. 10
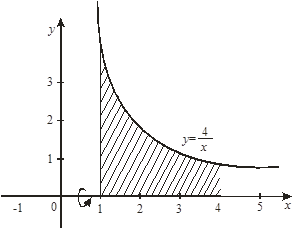
Рис. 11
Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной прямыми у = с и у = d, осью Оу и графиком непрерывной на отрезке ![]() функции
функции ![]() (рис. 12), определяется по формуле
(рис. 12), определяется по формуле
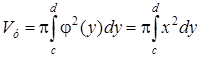 . (10)
. (10)
|
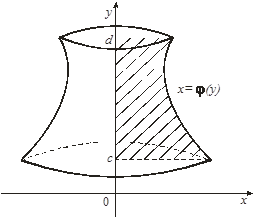
Рис. 12
Пример 14. Вычислить объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, ограниченной линиями х2 = 4у, у = 4, х = 0 (рис. 13).
Решение. В соответствии с условием задачи находим пределы интегрирования: ![]() ,
, ![]() . По формуле (10) получаем:
. По формуле (10) получаем:
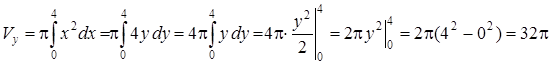 .
.
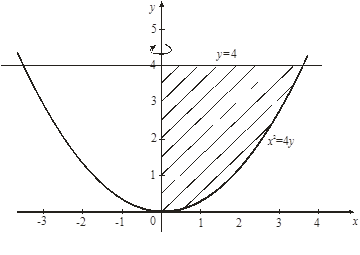
Рис. 13
3. Длина дуги плоской кривой
Пусть кривая ![]() , заданная уравнением
, заданная уравнением ![]() , где
, где ![]() , лежит в плоскости
, лежит в плоскости ![]() (рис. 14).
(рис. 14).
Рис. 14
Определение. Под длиной дуги ![]() понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю.
Если функция ![]() и ее производная
и ее производная ![]() непрерывны на отрезке
непрерывны на отрезке ![]() , то длина дуги кривой
, то длина дуги кривой ![]() вычисляется по формуле
вычисляется по формуле
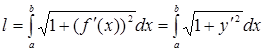 . (11)
. (11)
Пример 15. Вычислить длину дуги кривой ![]() , заключенной между точками, для которых
, заключенной между точками, для которых ![]() .
.
Решение. Из условия задачи имеем ![]() . По формуле (11) получаем:
. По формуле (11) получаем:
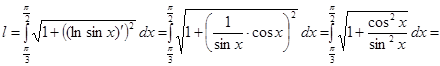
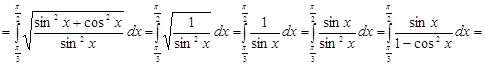
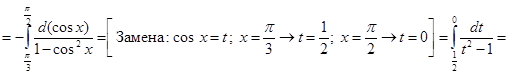
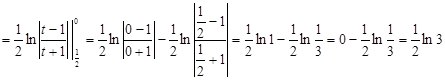 .
.
4. Несобственные интегралы с бесконечными пределами интегрирования
При введении понятия определённого интеграла 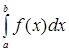 предполагалось, что выполняются следующие два условия:
предполагалось, что выполняются следующие два условия:
а) пределы интегрирования а и ![]() являются конечными;
являются конечными;
б) подынтегральная функция ![]() ограничена на отрезке
ограничена на отрезке ![]() .
.
Если хотя бы одно из этих условий не выполняется, то интеграл называется несобственным.
Рассмотрим вначале несобственные интегралы с бесконечными пределами интегрирования.
Определение. Пусть функция ![]() определена и непрерывна на промежутке
определена и непрерывна на промежутке ![]() , тогда
, тогда
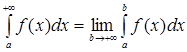 (12)
(12)
называется несобственным интегралом с бесконечным верхним пределом интегрирования (несобственным интегралом I рода).
Если 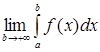 существует и конечен, то несобственный интеграл
существует и конечен, то несобственный интеграл 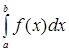 называется сходящимся; если данный предел не существует или равен
называется сходящимся; если данный предел не существует или равен ![]() , то несобственный интеграл называется расходящимся.
, то несобственный интеграл называется расходящимся.
Геометрически несобственный интеграл 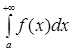 от неотрицательной функции
от неотрицательной функции ![]() выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции
выражает площадь бесконечной криволинейной трапеции, ограниченной сверху графиком функции ![]() , снизу – осью
, снизу – осью ![]() , слева – отрезком прямой
, слева – отрезком прямой ![]() и неограниченной справа (рис. 15).
и неограниченной справа (рис. 15).
Если несобственный интеграл сходится, то эта площадь является конечной; если несобственный интеграл расходится, то эта площадь бесконечна.
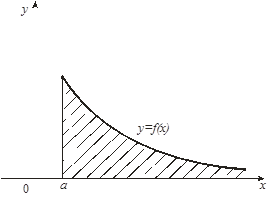
Рис. 15
Аналогично определяется несобственный интеграл с бесконечным нижним пределом интегрирования:
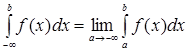 . (13)
. (13)
Этот интеграл сходится, если предел в правой части равенства (13) существует и конечен; в противном случае интеграл называется расходящимся.
Несобственный интеграл с двумя бесконечными пределами интегрирования определяется следующим образом:
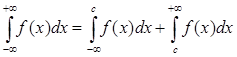 , (14)
, (14)
где с – любая точка интервала ![]() . Интеграл
. Интеграл 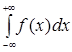 сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).
сходится только в том случае, когда сходятся оба интеграла в правой части равенства (14).
Пример 16. Исследовать на сходимость несобственные интегралы:
а) ![]() ; б)
; б)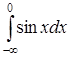 ; в)
; в) 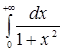 ; г)
; г) 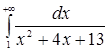 .
.
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
