Определенный интеграл
4. Формула Ньютона–Лейбница
Вычисление определенных интегралов через предел интегральных сумм связано с большими трудностями. Поэтому существует другой метод, основанный на тесной связи, существующей между понятиями определенного и неопределенного интегралов.
Теорема 2. Если функция которая называется формулой Ньютона–Лейбница. Разность где символ Таким образом, формулу (2) можно записать в виде:
Нахождение определенных интегралов с помощью формулы Ньютона-Лейбница осуществляется в два этапа: на первом этапе находят некоторую первообразную Пример 1. Вычислить интеграл Решение. Для подынтегральной функции Пример 2. Вычислить интеграл Решение. По формуле Ньютона-Лейбница имеем:
5. Замена переменной в определенном интеграле
Теорема 3. Пусть функция которая называется формулой замены переменной в определенном интеграле.
Заметим, что как и в случае неопределенного интеграла, использование замены переменной позволяет упростить исходный интеграл, приблизив его к табличному. При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования – достаточно лишь найти новые пределы интегрирования На практике часто вместо подстановки Пример 3. Вычислить интеграл Решение. Введем новую переменную по формуле Пример 4. Вычислить интеграл Решение. Воспользуемся универсальной тригонометрической подстановкой. Положим ![]() непрерывна на отрезке
непрерывна на отрезке ![]() – какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
– какая-либо ее первообразная на этом отрезке, то справедлива следующая формула:
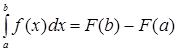 , (2)
, (2)
![]() принято записывать следующим образом:
принято записывать следующим образом:
![]() ,
,
![]() называется знаком двойной подстановки.
называется знаком двойной подстановки.
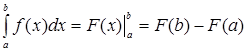 .
.
![]() для подынтегральной функции
для подынтегральной функции ![]() ; на втором – находится разность
; на втором – находится разность ![]() значений этой первообразной на концах отрезка
значений этой первообразной на концах отрезка ![]() .
.
![]() .
.
![]() произвольная первообразная имеет вид
произвольная первообразная имеет вид ![]() . Так как в формуле Ньютона-Лейбни-ца можно использовать любую первообразную, то для вычисления ин- теграла возьмем первообразную, имеющую наиболее простой вид:
. Так как в формуле Ньютона-Лейбни-ца можно использовать любую первообразную, то для вычисления ин- теграла возьмем первообразную, имеющую наиболее простой вид: ![]() . Тогда
. Тогда 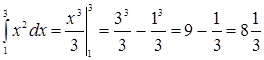 .
.
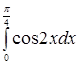 .
.
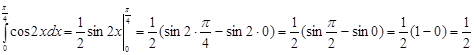 .
.
![]() непрерывна на отрезке
непрерывна на отрезке ![]() . Тогда, если: 1) функция
. Тогда, если: 1) функция ![]() и ее производная
и ее производная ![]() непрерывны при
непрерывны при ![]() ; 2) множеством значений функции
; 2) множеством значений функции ![]() при
при ![]() является отрезок
является отрезок ![]() ; 3)
; 3) ![]() ,
, ![]() , то справедлива формула
, то справедлива формула
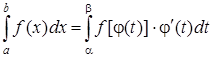 , (3)
, (3)
![]() и
и ![]() (для этого надо решить относительно переменной t уравнения
(для этого надо решить относительно переменной t уравнения ![]() и
и ![]() )).
)).
![]() используют подстановку
используют подстановку ![]() . В этом случае нахождение новых пределов интегрирования по переменной t упрощается:
. В этом случае нахождение новых пределов интегрирования по переменной t упрощается: ![]() ,
, ![]() .
.
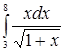
![]() . Определим
. Определим ![]() и
и ![]() . Возведя в квадрат обе части равенства
. Возведя в квадрат обе части равенства ![]() , получим
, получим ![]() , откуда
, откуда ![]()
![]() . Находим новые пределы интегрирования. Для этого в формулу
. Находим новые пределы интегрирования. Для этого в формулу![]() подставим старые пределы
подставим старые пределы ![]() и
и ![]() . Получим:
. Получим: ![]() , откуда
, откуда ![]() и, следовательно,
и, следовательно, ![]() ;
; ![]() , откуда
, откуда ![]() и, следовательно,
и, следовательно, ![]() . Таким образом:
. Таким образом:
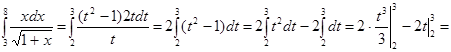
![]() .
.
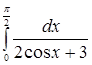 .
.
![]() , откуда
, откуда ![]()
![]() ,
, ![]() . Найдем новые пределы интегрирования: если
. Найдем новые пределы интегрирования: если ![]() , то
, то ![]() ; если
; если ![]() , то
, то ![]() . Значит,
. Значит, ![]() . Следовательно:
. Следовательно:
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
