Решение заданий по высшей математике

Содержание:

1. Система линейных уравнений. Определитель решения системы. Исследование линейной системы 2-ух уравнений с 2-мя неизвестными.

2. Определитель квадратной матрицы второго порядка. Формулы Крамера.

3. Определитель третьего порядка. Алгебраические дополнения, теорема о разложении определителя третьего порядка.

4. Матричное решение системы уравнений.

5. Исследовани

е систем линейных уравнений. Метод Гаусса.

6. Комплексные числа (определение). Мнимая единица. Форма записи.

7. Операции с комплексными числами (определение, свойства).

8. Геометрический смысл операций с комплексными числами.

9. Извлечение корня из комплексного числа.

10. Геометрическое изображение комплексного числа. Модуль и аргумент комплексного числа. Формула Муавра.

11. Основная теорема алгебры.

12. Прямоугольные координаты на плоскости. Расстояние между двумя точками плоскости.

13. Прямоугольные координаты на плоскости. Деление отрезка в данном отношении.

14. Прямоугольные координаты на плоскости. Уравнение окружности, уравнение эллипса.

15. Прямоугольные декартовы координаты в пространстве. Уравнение плоскости.

16. Элементы аналитической геометрии в пространстве. Уравнение плоскости.

17. Элементы аналитической геометрии в пространстве. Уравнение прямой.

18. Угол между плоскостями, расстояние от точки до плоскости.

19. Полярные координаты. Связь между прямоугольными и полярными координатами.

20. Понятие вектора. Линейные операции над векторами. Свойства.

21. Угол между двумя векторами. Проекция вектора на ось.

22. Линейная зависимость векторов.

23. Базис на плоскости и в пространстве. Аффинные координаты.

24. Направляющие косинусы

25.Скалярное произведение векторов.

26. Векторное произведение векторов.

27.Смешанное произведение векторов.

28. Функция одной переменной, график, способы задания.

29. Параметрический способ задания функции. Параметрическое уравнение окружности, эллипса.

30. Понятие сложной и обратной функции.

31. Четные, нечетные, периодические функции.

32. Классификация функций. Основные элементарные функции.

33. Числовые последовательности и пределы.

34. Бесконечно малая и бесконечно большая величина.

35. Предел функции на бесконечности.

36. Предел функции в точке.

37. Основные теоремы о пределах.

38. Бесконечно малые и бесконечно большие функции. Свойства бесконечно малых и их связь с бесконечно большими.

39. Вычисление некоторых пределов. Раскрытие неопределенностей

40. Первый замечательный предел.

41. Второй замечательный предел.

1. Система линейных уравнений. Определение решения линейной системы. Исследование линейной системы 2-х уравн. С 2-мя неизв.

Рассмотрим сист. 2-х уравн. С 2-мя неизв.

ì

ía11x1+a12x2=b1

î a21x1+a22x2=b2

Введем обозначение:

D=½a11 a12½

½a21 a22½

Dx1=½b1 a12½

½b2 a22½

Dx2=½a11 b1½

½ a21 b2½

D-это определитель, составленный из коэффициентов, стоящих перед неизв.

Определители Dx1 и Dx2 составл.из опред. D заменой столбца коэффициентов при соотв. перем. На столбец своб. Членов b1 и b2. Для нахождения неизв. x1 и x2 необх. Воспольз. Формулой:

x1=Dx1/D; x2=Dx2/D.

Итак, если D отличен от нуля, то система имеет единственное решение, опред. По данным фомулам, если D=0, то сист. Может иметь множ. Реш. Или их совсем не иметь.

Система m уравнений с n неизвестными в общем виде записывается следующим образом:

где aij – коэффициенты, а bi – постоянные.

Решениями системы являются n чисел, которые при подстановке в систему превращают каждое ее уравнение в тождество

система имеет хотя бы одно решение, то она называется совместной. Если система не имеет ни одного решения, то она называется несовместной.

Система называется определенной, если она имеет только одно решение и неопределенной, если более одного.

2. Определитель квадратной матрицы 2-го порядка. Формулы Крамера.

Любые 4 числа, расположенные в виде квадратной таблицы, называются квадратной матрицей второго порядка. Каждой квадратной матрице 2-ого порядка можно поставить в соответствие число, называемое её определителем и обозначаемое D=|A|.

Определитель матр. 2-го порядка равен числу

a11· a22-a21·a12

Св-ва опред. 2-го порядка:

1. опред. Не измен. Если его строки поменять местами с соотв. столбцами

2. при перестановки 2-х строк(или столбцов) опред. Изменит знак на противоп.

3. опред. С двумя одинак. Строками или столб. Равен нулю

4. общий множит. Всех элем. Строки или столбца можно выносить за знак опред.

5. если все элем. Какой-л. строки(ст.) равны нулю, то опред. Равен нулю

6. если к элем. К-л. строки или столб. Опред. Приб. В соотв. элем. Др. строки или ст., умножен. На одно и то же число, то опред не изм.

7. опред. Равен алгебр. Сумме произв. Элем. К.-л. строки (ст) на их алгебр. Доп.

Теорема Крамера

Данный метод также применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.

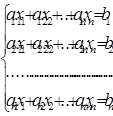
Система из n уравнений с n неизвестнымив случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:xi = Di/D, где D = опред. Матр., а Di – определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов

Если система однородна, т.е. bi = 0, то при D¹0 система имеет единственное нулевое решение x1 = x2 = … = xn = 0.При D = 0 система имеет бесконечное множество решений.

3. Определитель 3-го порядка. Алгебраические дополнения, теорема о разложении определителя третьего порядка.

9 элементов aij, где i-номер строка, а j-номер столбца, располагаются в квадратную таблицу, называемую квадратной матрицей третьего порядка. Ей можно поставить в соответствие число, которое называется определителем 3-го порядка.

Опред. Равен алгебр. Сумме произв. Элем. К.-л. строки (ст.) на их алгебр. Доп.

Алгебраическое дополнение Aij для элемента aij – число равное

(-1) i+jMij, где Mij минор элемента aij.

Минор Mij элемента Aij матрицы А наз-ся определитель, полученный из исходного определителя А вычеркиванием итой строки и житого столбца.

4. Матричное решение системы уравнений

Рассмотрим систему n линейных уравнений с n неизвестными.

Рассмотрим 3 матрицы, связанный одной системой

 Скачать реферат