Преобразование Лапласа

Рефераты / Математика / Преобразование Лапласа

· Условия существования обратного преобразования Лапласа

Для существования обратного преобразования Лапласа достаточно выполнение следующих условий:

1. Если изображение F(s) — аналитичная функция для $\sigma \geqslant \sigma_a$ и имеет порядок меньше −1, то обратное преобразование для неё

существует и непрерывно для всех значений аргумента, причём

$\mathcal{L}^{-1} \{F(s) \} = 0$ для $t \leqslant 0$

2. Пусть

$F(s) = \varphi[F_1(s), F_2(s), \dots, F_n(s)]$ ,

так что $\varphi(z_1, z_2, \dots, z_n)$

аналитична относительно каждого zk и равна нулю для

$z_1 = z_2 = \dots = z_n = 0$ , и

$F_k(s) = \mathcal{L} \{f_k(x) \{ (\sigma > \sigma_{ak}\colon k = 1, 2, \dots, n)$

тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.

Примечание: это достаточные условия существования.

· Теорема о свёртке

Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.

$\mathcal{L} \{ f(x) * g(x) \} = \mathcal{L} \{ f(x) \} \cdot \mathcal{L} \{ g(x) \}$

· Умножение изображений

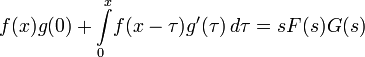
$f(x)g(0) + \int\limits_{0}^{x}\limits\! f(x-\tau)g'(\tau)\,d\tau = sF(s)G(s)$

Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.

· Дифференцирование и интегрирование оригинала

Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.

$\mathcal{L} \{f'(x)\} = s \cdot F(s) - f(0^+)$

В более общем случае (производная n-го порядка):

$\mathcal{L}\left\{ f^{(n)} (x) \right\} = s^n \cdot F(s) - s^{n - 1} f(0^+) - \dots - f^{(n - 1)}(0^+)$

Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.

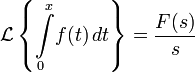
$\mathcal{L} \left\{ \int\limits_{0}^{x}\limits\! f(t)\,dt \right\} = \frac{F(s)}{s}$

· Дифференцирование и интегрирование изображения. Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.

$\mathcal{L}^{-1} \{F'(s)\} = -xf(x)$

Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент.

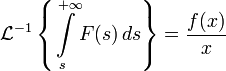
$\mathcal{L}^{-1} \left\{ \int\limits_{s}^{+\infty}\limits\! F(s)\,ds \right\} = \frac{f(x)}{x}$

· Запаздывание оригиналов и изображений. Предельные теоремы

Запаздывание изображения:

$\mathcal{L}\left\{ e^{ax} f(x) \right\} = F(s - a)$

$\mathcal{L}^{-1} \left\{ F(s - a) \right\} = e^{ax} f(x)$

Запаздывание оригинала:

$\mathcal{L}\left\{ f(t - a) u(t - a) \right\} = e^{-as} F(s)$

$\mathcal{L}^{-1} \left\{ e^{-as} F(s) \right\} = f(x - a) u(x - a)$

Примечание: u(x) — Функция Хэвисайда.

Теоремы о начальном и конечном значении (предельные теоремы):

$f(\infty)=\lim_{s\to 0}{sF(s)}$

Все полюсы в левой полуплоскости. Теорема о конечном значении очень полезна, так как описывает поведение оригинала на бесконечности с помощью простого соотношения. Это, к примеру, используется для анализа устойчивости траектории динамической системы.

$\lim_{s\to \infty}{sF(s)} = f(0 + 0)= \!$

· Другие свойства

Линейность

$\mathcal{L}\left\{a f(x) + b g(x) \right\} = a F(s) + b G(s)$

Умножение на число

$\mathcal{L} \left\{ f(ax) \right\} =\frac{1}{a} F \left (\frac{s}{a}\right )$

6. Прямое и обратное преобразование Лапласа некоторых функций

Ниже представлена таблица преобразования Лапласа для некоторых функций.

№	Функция	Временная область $x(t) = \mathcal{L}^{-1} \left\{ X(s) \right\}$	Частотная область $X(s) = \mathcal{L}\left\{ x(t) \right\}$	Область сходимости для причинных систем
1	идеальное запаздывание	$\delta(t-\tau) \$	$e^{-\tau s} \$
1а	единичный импульс	$\delta(t) \$	$1 \$	$\mathrm{all} \ s \,$
2	запаздывание n-го порядка с частотным сдвигом	$\frac{(t-\tau)^n}{n!} e^{-\alpha (t-\tau)} \cdot u(t-\tau)$	$\frac{e^{-\tau s}}{(s+\alpha)^{n+1}}$	$s > 0 \,$
2а	степенная n-го порядка	${ t^n \over n! } \cdot u(t)$	${ 1 \over s^{n+1} }$	$s > 0 \,$
2а.1	степенная q-го порядка	${ t^q \over \Gamma(q+1) } \cdot u(t)$	${ 1 \over s^{q+1} }$	$s > 0 \,$
2а.2	единичная функция	$u(t) \$	${ 1 \over s }$	$s > 0 \,$
2b	единичная функция с запаздыванием	$u(t-\tau) \$	${ e^{-\tau s} \over s }$	$s > 0 \,$
2c	«ступенька скорости»	$t \cdot u(t)\$	$\frac{1}{s^2}$	$s > 0 \,$
2d	n-го порядка с частотным сдвигом	$\frac{t^{n}}{n!}e^{-\alpha t} \cdot u(t)$	$\frac{1}{(s+\alpha)^{n+1}}$	$s > - \alpha \,$
2d.1	экспоненциальное затухание	$e^{-\alpha t} \cdot u(t) \$	${ 1 \over s+\alpha }$	$s > - \alpha \$
3	экспоненциальное приближение	$( 1-e^{-\alpha t}) \cdot u(t) \$	$\frac{\alpha}{s(s+\alpha)}$	$s > 0\$
4	синус	$\sin(\omega t) \cdot u(t) \$	${ \omega \over s^2 + \omega^2 }$	$s > 0 \$
5	косинус	$\cos(\omega t) \cdot u(t) \$	${ s \over s^2 + \omega^2 }$	$s > 0 \$
6	гиперболический синус	$\sinh(\alpha t) \cdot u(t) \$	${ \alpha \over s^2 - \alpha^2 }$	$s > \| \alpha \| \$
7	гиперболический косинус	$\cosh(\alpha t) \cdot u(t) \$	${ s \over s^2 - \alpha^2 }$	$s > \| \alpha \| \$
8	экспоненциально затухающий синус	$e^{-\alpha t} \sin(\omega t) \cdot u(t) \$	${ \omega \over (s+\alpha )^2 + \omega^2 }$	$s > -\alpha \$
9	экспоненциально затухающий косинус	$e^{-\alpha t} \cos(\omega t) \cdot u(t) \$	${ s+\alpha \over (s+\alpha )^2 + \omega^2 }$	$s > -\alpha \$
10	корень n-го порядка	$\sqrt[n]{t} \cdot u(t)$	$s^{-(n+1)/n} \cdot \Gamma\left(1+\frac{1}{n}\right)$	$s > 0 \,$
11	натуральный логарифм	$\ln \left ( { t \over t_0 } \right ) \cdot u(t)$	$- { t_0 \over s} \ [ \ \ln(t_0 s)+\gamma \ ]$	$s > 0 \,$
12	функция Бесселя первого рода порядка n	$J_n( \omega t) \cdot u(t)$	$\frac{ \omega^n \left(s+\sqrt{s^2+ \omega^2}\right)^{-n}}{\sqrt{s^2 + \omega^2}}$	$s > 0 \,$ $(n > -1) \,$
13	модифицированная функция Бесселя первого рода порядка n	$I_n(\omega t) \cdot u(t)$	$\frac{ \omega^n \left(s+\sqrt{s^2-\omega^2}\right)^{-n}}{\sqrt{s^2-\omega^2}}$	$s > \| \omega \| \,$
14	функция Бесселя второго рода нулевого порядка	$Y_0(\alpha t) \cdot u(t)$
15	модифицированная функция Бесселя второго рода, нулевого порядка	$K_0(\alpha t) \cdot u(t)$
16	функция ошибок	$\mathrm{erf}(t) \cdot u(t)$	${e^{s^2/4} \operatorname{erfc} \left(s/2\right) \over s}$	$s > 0 \,$