Преобразование Лапласа
Примечания к таблице:
· ![]() — функция Хэвисайда.
— функция Хэвисайда.
· ![]() — дельта-функция.
— дельта-функция.
· ![]() — гамма-функция.
— гамма-функция.
· ![]() — постоянная Эйлера — Маскерони.
— постоянная Эйлера — Маскерони.
· ![]() , — вещественная переменная.
, — вещественная переменная.
· ![]() — комплексная переменная.
— комплексная переменная.
· ![]() ,
, ![]() ,
, ![]() и
и ![]() — вещественные числа.
— вещественные числа.
· ![]() — целое число.
— целое число.
Причинная система — система, в которой импульсная передаточная функция h(t) равна нулю для любого момента времени ![]() .
.
7. Применения преобразования Лапласа
Преобразование Лапласа находит широкое применение во многих областях математики (операционное исчисление), физики и техники.
· Решение систем дифференциальных и интегральных уравнений с помощью преобразования Лапласа легко переходить от сложных понятий математического анализа к простым алгебраическим соотношениям.
· Расчёт передаточных функций динамических систем, таких, к примеру, как аналоговые фильтры.
· Расчёт выходных сигналов динамических систем в теории управления и обработке сигналов — так как выходной сигнал линейной стационарной системы равен свёртке её импульсной характеристики с входным сигналом, преобразование Лапласа позволяет заменить эту операцию на простое умножение.
· Расчёт электрических схем. Производится путём решения дифференциальных уравнений, описывающих схему операторным методом.
· Решение нестационарных задач математической физики.
8. Связь с другими преобразованиями
Фундаментальные связи
Практически все интегральные преобразования имеют схожую природу и могут получаться одно из другого через выражения соответствия. Многие из них являются частными случаями других преобразований. Далее даны формулы, связывающие преобразования Лапласа с некоторыми другими функциональными преобразованиями.
Преобразование Лапласа-Карсона
Преобразование Лапласа-Карсона получается из преобразования Лапласа путём домножения его на комплексную переменную.
![]()
Двустороннее преобразование Лапласа
Двустороннее преобразование Лапласа ![]() связано с односторонним с помощью следующей формулы:
связано с односторонним с помощью следующей формулы:
![]()
Преобразование Фурье
Непрерывное преобразование Фурье эквивалентно двустороннему преобразованию Лапласа с комплексным аргументом s = iω:
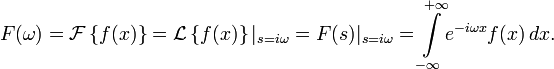
Примечание: в этих выражениях опущен масштабирующий множитель
![]()
который часто включается в определения преобразования Фурье.
Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.
Преобразование Меллина
Преобразование Меллина и обратное преобразование Меллина связаны с двусторонним преобразованием Лапласа простой заменой переменных. Если в преобразовании Меллина
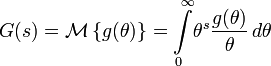
положим θ = e − x, то получим двустороннее преобразование Лапласа.
Z-преобразование
Z-преобразование — это преобразование Лапласа решётчатой функции, производимое с помощью замены переменных:
![]()
где ![]() — период дискретизации, а
— период дискретизации, а ![]() — частота дискретизации сигнала. Связь выражается с помощью следующего соотношения:
— частота дискретизации сигнала. Связь выражается с помощью следующего соотношения:
![]()
Преобразование Бореля
Интегральная форма преобразования Бореля идентична преобразованию Лапласа, существует также обобщённое преобразование Бореля, с помощью которого использование преобразования Лапласа распространяется на более широкий класс функций.
9. Преобразование Лапласа по энергии
Запишем уравнение
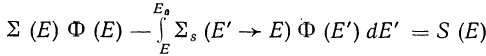
для моноэнергетического источника S(E)=d(E-E0) с интегральным членом в форме:

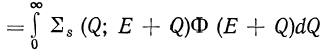
и, не пренебрегая для простоты зависимостью сечений Σ(E) и
![]()
от E, перейдем от E к новой переменной
D=![]() :
:
![]()
Ф(D)=Ф(E)![]() (1)
(1)
Решение этого уравнения можно получить с помощью преобразования Лапласа по энергии:
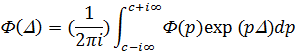 (2)
(2)
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
