Преобразование Лапласа
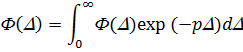 (3)
(3)
Его можно рассматривать как разложение дифференциальной плотности потока по системе биортогональной функции ![]() и
и ![]() .
.
Подействуем на все члены уравнения (1) оператором <
p>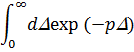
В соответствии с (3) первый член преобразования к виде
![]()
Во втором члене необходимо изменить порядок интегрирования и в интеграле по D сделать замену переменных
![]()
Тогда он приведется к виду
![]() ,
,
где ![]() (4)
(4)
-трансформанта Лапласа от дифференциального сечения рассеяния.
Правая часть уравнения (1) легко преобразуется, после чего получаем
![]() ’
’
Откуда
![]() . (5)
. (5)
Подставляя (5) в (2), находим интересующую нас функцию Ф(D):
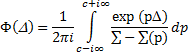
Если сечение
![]()
быстро убывает с ростом Q экспоненту в (4) можно разложить в ряд.
Тогда
![]()
где ![]() -середина потери энергии на единице длины пути. Подставим это разложение в (6) и сделаем замену переменных
-середина потери энергии на единице длины пути. Подставим это разложение в (6) и сделаем замену переменных
![]()
Тогда (6) перейдет в:
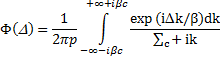
Вычисляя, интеграл с помощью вычетов и возвращаясь от переменной ![]() к переменной E, получаем:
к переменной E, получаем:
![]() (7)
(7)
Экспонента в формуле (7) есть вероятность того, что частица избежит поглощения на пути, где энергия меняется от Е0 до Е. Если сечение поглощения равно нулю, то
![]() (8)
(8)
Формула (8) имеет простой физический смысл. По определению Ф(E)=dE есть средний путь, пройденный частицей за время, пока ее энергия меняется от E+dE до E.
В приближении непрерывного замедления dE/dl=b, откуда dl/dE=1/b, что совпадает с (8).
10. Преобразование Лапласа по координатам
Запишем кинетическое уравнение в приближении «прямо-вперед» (т.е. без учета отклонения частиц при рассеянии), для частиц, испускаемых моноэнергетическим источником, который находится в начале координат:
![]() (208)
(208)
![]() (209)
(209)
Поскольку частицы испускаются в положительном направлении оси Оz, в области z<0 плотность потока равна 0 и область изменения z в уравнении (208) следует считать полубесконечный интервал (0,¥). Это обстоятельство позволяет применить для решения уравнения (208) преобразование Лапласа по координатам:
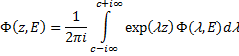 (210)
(210)
где трансформанта Лапласа Ф(l,E) выражается через плотность потока следующим образом:
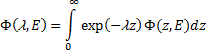 (211)
(211)
Умножим обе части уравнения (208) на ![]() и проинтегрируем по z от 0 до ¥. Преобразовав первый член интегрированием по частям с учетом граничного условия (209) и, использовав обозначение (211), получим:
и проинтегрируем по z от 0 до ¥. Преобразовав первый член интегрированием по частям с учетом граничного условия (209) и, использовав обозначение (211), получим:
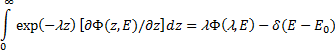
После преобразования Лапласа остальных членов уравнения (208) приходим к уравнению для трансформанты плотности потока:
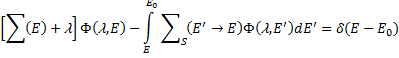 (212)
(212)
которое в отличие от (208) не содержит производных и является интегральным уравнением типа уравнения деградации энергии. Введя обозначение
![]() (213)
(213)
Перепишем уравнение (312) в виде
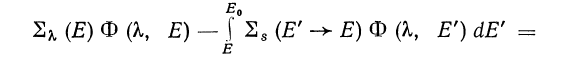
![]() (214)
(214)
При действительных ![]() уравнение (214) по форме совпадает с уравнением деградации энергии для частиц с макроскопическим сечением столкновений
уравнение (214) по форме совпадает с уравнением деградации энергии для частиц с макроскопическим сечением столкновений ![]() и дифференциальным сечением рассеяния
и дифференциальным сечением рассеяния
![]()
Из (213) видно, что по мере уменьшения l ![]() обращается в нуль, а потом становится отрицательной. Отсюда следует, что решение уравнения (214) существует лишь в области
обращается в нуль, а потом становится отрицательной. Отсюда следует, что решение уравнения (214) существует лишь в области
![]()
Если выполняется условие
![]()
то для трансформанты рассеянной компоненты плотности потока получим
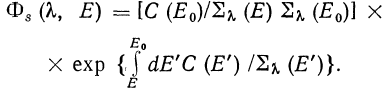 (215)
(215)
Если ![]() и C не зависят от энергии, формула (215) упрощается:
и C не зависят от энергии, формула (215) упрощается:
![]() (216)
(216)
Перейдем к восстановлению энергетического спектра рассеянных частиц:
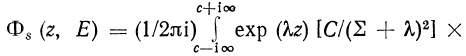
![]() (217)
(217)
гдеRel=C>-![]()
Введем обозначения
![]()
Тогда формула (217) примет вид:
![]()
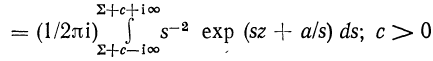 (218)
(218)
Функция ![]() , представляющая собой обратное преобразование Лапласа функции s-2exp(a/s),равна
, представляющая собой обратное преобразование Лапласа функции s-2exp(a/s),равна
![]() '
'
где I1- модифицированная функция Бесселя первого порядка. Таким образом
![]()
Другие рефераты на тему «Математика»:
Поиск рефератов
Последние рефераты раздела
- Анализ надёжности и резервирование технической системы
- Алгоритм решения Диофантовых уравнений
- Алгебраическое доказательство теоремы Пифагора
- Алгоритм муравья
- Векторная алгебра и аналитическая геометрия
- Зарождение и создание теории действительного числа
- Вероятностные процессы и математическая статистика в автоматизированных системах
