Основные положения дискретной математики

Записывается граф следующим образом: G(V,E).

Элементы множества V называются вершинами графа G. Элементы множества Е – ребрами графа G. Вершины и ребра графа G называют его элементами и часто записывают и .

7.1 Понятие смежности

Пусть v1, v2 – вершин

ы, е1 – соединяющее их ребро. Тогда вершина v1 и ребро е1 – инцидентны, вершина v2 и ребро е1 также инцидентны. Два ребра инцидентные одной вершине (е1,е2 инцидентны v2) называются смежными. А также две вершины инцидентные одному ребру (v1, v2 инцидентны е1 называются смежными.

Пример: обычно граф изображают диаграммой: вершины – точками (или кружками), ребра – линиями. Изобразим граф, имеющий 4 вершины и 5 ребер.

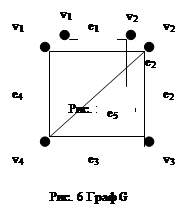Пример: Задание: выписать все смежные и несмежные вершины и ребра.

Решение:

Таб.7

До настоящего момента мы рассматривали неориентированный граф. Если каждому ребру графа присвоить направление (в виде стрелочки) от одной вершины к другой, то такие ребра называются дугами, а содержащий их граф называется ориентированным (или орграфом).

Первая по порядку вершина инцидентная дуге ориентированного графа, называется его началом, вторая – его концом.

Вершины в ориентированном графе называются узлами.

Рассмотрим некоторые виды графов:

· Если ребро соединяет вершину саму с собой, то такой элемент графа называется петлей, а содержащий его граф называется графом с петлей (или псевдографом):

· Если различные ребра могут быть инцидентными одной паре вершин, то они называются кратными, а содержащий их граф называется мультиграфом:

· Множество ребер Е может быть пустым:

· Линии, изображающие ребра графа могут пересекаться, но точки пересечения не являются вершинами:

·

· Граф может быть бесконечным:

Каждому неориентированному графу можно поставить в соответствие орграф с тем же множеством вершин заменив лишь ребра неориентированного графа на направленные дуги орграфа. Такое соответствие называется каноническим.

7.2 Матрица инцидентности и списки ребер

Задать граф – значит описать множества его вершин и ребер, а также отношение инцидентности. Когда граф конечен для описания его вершин и ребер достаточно их занумеровать. Отношение инцидентности определяют матрицей ij, имеющей m строк и n столбцов. Столбцы соответствуют вершинам графа, строки – ребрам графа. Если ребро еi инцидентно вершине vj, то ij = 1, в противном случае ij = 0. Это матрица инцидентности для неориентированного графа.

Пример (Задание №9)

Обозначим вершины римскими цифрами, а ребра – арабскими. Матрица инцидентности для данного графа выглядит следующим образом:

 Скачать реферат