Основные положения дискретной математики

Доказательство производится в два этапа: 1) «в одну сторону», 2) «в обратную сторону».

1) Сначала предположим, что некий элемент х принадлежит левой части равенства: эта запись звучит следующим образом:

«если , то ».

2) На втором этапе предполагается, что элемент х принадлежит правой части равенства: .

Пример №1

Доказать тождество:

.

Решение:

1) ;

2) .

1.5 Отношения на множествах

Отношения бывают одноместными, двуместными (бинарными) и n-местными. Одноместное отношение– это просто подмножество. Мы остановимся на бинарных отношениях.

1. упорядоченная пара (x, y) есть совокупность двух элементов записанных в определенном порядке.

2. Две пары (x, y) и (x1, y1) считаются равными тогда и только тогда x1 = х, y1 = y.

3. Прямым произведением x y называется совокупность пар (x,y)таких, что .

Можно привести следующие примеры бинарных отношений:

· Отношение «иметь общий делитель отличный от 1» выполняется для пар (6,9); (4,2); (2,4); (4,4), но не выполняется для пар (7,9); (4,7).

· Отношение «быть делителем», т. е. x делит y выполняется для пар (2,4); (4,4), но не выполняется для пар (4,2); (7,9).

· Отношение выполняется для пар (7,9); (7,7), но не выполняется для пары (9,7).

1.6 Свойства отношений

1. Рефлексивность;

2. Симметричность;

3. Транзитивность.

Отношение обозначается R и записывается так: xRy (x и y находятся в отношении R).

Отношение R называется рефлективным, если для любого имеет место aRa. Главная диагональ его матрицы содержит только единицы.

Отношение R называется антирефлективным, если для любого не выполняется aRa. Главная диагональ его матрицы содержит только нули. Отношения = - рефлективные, а отношение < - антирефлективное.

Отношение R называется симметричным, если для пары (а,в)из aRb следует bRa, иначе говоря для любой пары отношение выполняется либо в обе стороны, либо не выполняется вообще. Матрица данного отношения симметрична относительно главной диагонали.

Отношение R называется транзитивным, если для любых a,b,c из aRb и bRс следует aRс отношения = - транзитивны, отношение «пересекаться» – нетранзитивно. (Пример: пересекается с пересекается с , однако и не пересекаются).

Задание №2

Установите какими свойствами обладает каждое из отношений, заданных на R следующими высказывательными формами:

a) x+y=2;

Решение:

в данном случае заданы отношения + и .

Подставим в выражение x+y=2 конкретные значения: 1+1=2, последовательно проверим каждое свойство:

Рефлективность: aRа = а+а = 1+1 – условие выполняется , следовательно данное отношение рефлективно.

Симметричность: из aRb следует bRa = из а+b следует b+а = из 1+1 следует 1+1 – условие выполняется, следовательно данное отношение симметрично.

Транзитивность: из aRb и bRс следует aRс данное условие мы проверит не можем, т. к. оно применимо только для трех или более элементов.

1.7 Декартово произведение множеств

Декартовым произведением – XY множеств X и Y называется множество М вида

В круглых скобках обозначена последовательность, т. е. множество, в котором зафиксирован порядок элементов.

Подмножество FXY называется функцией, если для каждого элемента xX, найдется не более одного элемента yY вида (x,y) F; при этом, если для каждого элемента х имеется один элемент y вида (x,y) F, то функция называется всюду (полностью) определенной, в противном случае – частично определенной (не доопределенной).

Множество Х образует область определения функции F.

Множество Y образует область значений функции F.

Часто вместо (x,y) F пишут у=F(х), при этом элемент х называется аргументом или переменной, а у – значением функции F.

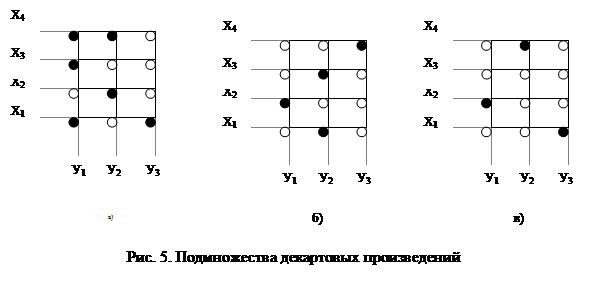
Сопоставим с декартовым произведением двух множеств х=. и у=. прямоугольную решетку, узлы которой взаимно однозначно соответствуют элементам декартова произведения (рис.5).

Подмножества декартова произведения обозначены штриховкой соответствующих элементов.

На рис.5 а) показано подмножество декартова произведения не являющееся функцией.

На рис.5 б) показано подмножество декартова произведения, являющееся полностью определенной функцией.

На рис. 5 в) показано подмножество декартова произведения, являющееся частично определенной функцией.

Количество аргументов определяет местность функции. До настоящего момента были рассмотрены одноместные функции.

Аналогично понятию декартова произведения двух множеств можно определить понятие декартова произведения n-множеств.

Декартовым произведением множеств М1, М2,…., Мn называется множество Элементами декартова произведения являются всевозможные последовательности, каждая из которых состоит из n элементов, причем первый элемент принадлежит множеству М1, второй – множеству М2, n-ый – множеству Мn.

 Скачать реферат