Основные положения дискретной математики

В матрице инцидентности орграфа ij = -1, если вершина vj – начало дуги ai; ij = 1, если vj – конец дуги ai; если ai – петля, а vj – инцидентная ей вершина, то ij = а, где а – любое число отличное от 0, 1

, -1. В остальных случаях ij = 0.

Пример (Задание №10): построим ориентированный граф и матрицу инцидентности для нее:

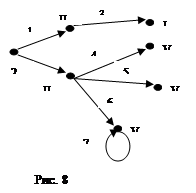
Из матрицы инцидентности мы видим, что в каждой строке есть только два элемента (или один, если ребро является петлей) отличных от 0. Поэтому такой способ задания графа посчитали неэкономичным. Отношение инцидентности можно задать так же с помощью списков ребер графа. Каждая строка этого списка соответствует ребру, в ней записывают номера вершин, инцидентных ему. Для неориентированного графа порядок вершин в строке произволен, а для орграфа первым записывают номер вершины начала дуги, а вторым – номер вершины конца дуги.

Составим списки ребер для данных графов:

Таб. 8 Списки ребер неориентированного графа

Таб. 9 Списки ребер орграфа

Каждая строка списка ребер соответствует строке матрицы с тем же номером ребра.

7.3 Матрица смежности графа

Матрица смежности – это квадратная матрица ij, строкам и столбцам которой соответствуют вершины графа. Для неориентированного графа ij ровно количеству ребер, инцидентных i-ой и j-ой вершинам. Для орграфа ij ровно количеству ребер с началом в i-ой вершине и концом j-ой вершине. Таким образом матрица смежности неориентированного графа симметрична, а орграфа – необязательно.

Пример: построим матрицы смежности для графов, рассмотренных ранее.

 Скачать реферат