Непрерывность функции на интервале и на отрезке

Рефераты / Математика / Непрерывность функции на интервале и на отрезке

Аналогично доказывается, что $ f(x)$ограничена снизу, откуда следует утверждение теоремы.

Очевидно, что ослабить условия теоремы нельзя: если функция не является непрерывной, то она не обязана быть ограниченной на отрезке (приведём в качестве примера функцию

$\displaystyle f(x)=\left\{\begin{array}{ll} \dfrac{1}{x},&\mbox{ при }x\ne0;\\ 0,&\mbox{ при }x=0, \end{array}\right. $

на отрезке $ [-1;1]$. Эта функция не ограничена на отрезке, так как при $ x=0$имеет точку разрыва второго рода, такую что $ \vert f(x)\vert\to+\infty$при $ x\to0$. Также нельзя заменить в условии теоремы отрезок интервалом или полуинтервалом: в качестве примера рассмотрим ту же функцию $ f(x)$на полуинтервале $ (0;1]$. Функция непрерывна на этом полуинтервале, но неограничена, вследствие того что $ f(x)\to+\infty$при $ x\to0+$.

Поиск наилучших постоянных, которыми можно ограничить функцию сверху и снизу на заданном отрезке, естественным образом приводит нас к задаче об отыскании минимума и максимума непрерывной функции на этом отрезке. Возможность решения этой задачи описывается следующей теоремой.

Теорема 3.9 (о достижении экстремума непрерывной функцией) Пусть функция $ f(x)$непрерывна на отрезке $ [a;b]$. Тогда существует точка $ x_*\in[a;b]$, такая что $ f(x_*)\leqslant f(x)$при всех $ x\in[a;b]$(то есть $ x_*$- точка минимума: $ f(x_*)=\min\limits_{x\in[a;b]}f(x)$), и существует точка $ x_{**}\in[a;b]$, такая что $ f(x_{**})\geqslant f(x)$при всех $ x\in[a;b]$(то есть $ x_{**}$- точка максимума: $ f(x_{**})=\max\limits_{x\in[a;b]}f(x)$). Иными словами, минимальное и максимальное8 значения непрерывной функции на отрезке существуют и достигаются в некоторых точках $ x_*$и $ x_{**}$этого отрезка.

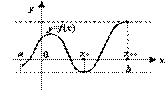
Рис.3.24. Непрерывная на отрезке функция достигает максимума и минимума

Доказательство. Так как по предыдущей теореме функция $ f(x)$ограничена на $ [a;b]$сверху, то существует точная верхняя грань значений функции на $ [a;b]$- число $ K=\sup\limits_{x\in[a;b]}\{f(x)\}$. Тем самым, множества $ M_1=\{x\in[a;b]:f(x)\geqslant K-1\}$, $ {M_2=\{x\in[a;b]:f(x)\geqslant K-\frac{1}{2}\}}$, ., $ M_i=\{x\in[a;b]:f(x)\geqslant K-\frac{1}{i}\}$, ., не пусты, и по предыдущей лемме в них есть наименьшие значения $ x_i$: $ f(x_i\geqslant K-\frac{1}{i}$, $ i=1,2,\dots$. Эти $ x_i$не убывают (доказывается это утверждение точно так же, как в предыдущей теореме):

$\displaystyle x_1\leqslant x_2\leqslant x_3\leqslant \dots\leqslant x_i\leqslant \dots,$

и ограничены сверху числом $ b$. Поэтому, по теореме о пределе монотонной ограниченной последовательности, существует предел $ \lim\limits_{i\to\infty}x_i=x_{**}.$Так как $ f(x_i)\geqslant K-\frac{1}{i}$, то и

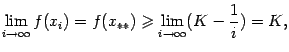
$\displaystyle \lim\limits_{i\to\infty}f(x_i)=f(x_{**})\geqslant \lim\limits_{i\to\infty}(K-\frac{1}{i})=K,$

по теореме о переходе к пределу в неравенстве, то есть $ f(x_{**})\geqslant K$. Но при всех $ x\in[a;b]$$ f(x)\leqslant K$, и в том числе $ f(x_{**})\leqslant K$. Отсюда получается, что $ f(x_{**})=K$, то есть максимум функции достигается в точке $ x_{**}$.

Аналогично доказывается существование точки минимума.

В этой теореме, как и в предыдущей, нельзя ослабить условия: если функция не является непрерывной, то она может не достигать своего максимального или минимального значения на отрезке, даже будучи ограниченной. Для примера возьмём функцию

Скачать реферат Скачать реферат
Страница:  1  2  3  4  5  6 


Другие рефераты на тему «Математика»:

Поиск рефератов

Последние рефераты раздела

Copyright © 2010-2024 - www.refsru.com - рефераты, курсовые и дипломные работы